There is a conical pipe of radii of its two ends as 0.2m and 0.02m with 20 N/m2 as the pressure difference along its length. A liquid of density 1.00×103kg/m3 is flowing through the pipe. Calculate the rate of flow of liquid through the pipe.
To solve the problem, we will follow these steps:
Step 1: Understand the Given Information
We have a conical pipe with:
- Radius at end A (R_A) = 0.2 m
- Radius at end B (R_B) = 0.02 m
- Pressure difference (ΔP) = P_B - P_A = 20 N/m²
- Density of the liquid (ρ) = 1.00 x 10³ kg/m³
Step 2: Apply the Continuity Equation
The continuity equation states that the mass flow rate must be constant throughout the pipe. This can be expressed as:
AAVA=ABVB
Where:
- AA=πR2A (Area at end A)
- AB=πR2B (Area at end B)
Calculating the areas:
- AA=π(0.2)2=0.04πm2
- AB=π(0.02)2=0.0004πm2
Using the continuity equation:
0.04πVA=0.0004πVB
Cancelling π:
0.04VA=0.0004VB
VA=0.01VB
Step 3: Apply Bernoulli's Equation
Bernoulli's equation relates the pressure and velocity at two points along the streamline:
PA+12ρV2A=PB+12ρV2B
Rearranging gives:
PB−PA=12ρ(V2A−V2B)
Substituting the known values:
20=12(1.00×103)(V2A−V2B)
Step 4: Substitute VA in Terms of VB
Using VA=0.01VB:
20=12(1.00×103)((0.01VB)2−V2B)
20=12(1.00×103)(0.0001V2B−V2B)
20=12(1.00×103)(−0.9999V2B)
20=−499.95V2B
V2B=−20−499.95≈0.04001
VB≈√0.04001≈0.200m/s
Step 5: Calculate VA
Using VA=0.01VB:
VA=0.01×0.200≈0.002m/s
Step 6: Calculate the Volume Flow Rate Q
Using the formula for volume flow rate:
Q=ABVB
Substituting the values:
Q=0.0004π×0.200
Q≈0.0004×3.1416×0.200≈0.000251m3/s
Final Answer
The rate of flow of liquid through the pipe is approximately:
Q≈2.51×10−4m3/s
---
We have a conical pipe with:
- Radius at end A (R_A) = 0.2 m
- Radius at end B (R_B) = 0.02 m
- Pressure difference (ΔP) = P_B - P_A = 20 N/m²
- Density of the liquid (ρ) = 1.00 x 10³ kg/m³
The continuity equation states that the mass flow rate must be constant throughout the pipe. This can be expressed as:
AAVA=ABVB
Where:
- AA=πR2A (Area at end A)
- AB=πR2B (Area at end B)
- AA=π(0.2)2=0.04πm2
- AB=π(0.02)2=0.0004πm2
0.04πVA=0.0004πVB
Cancelling π:
0.04VA=0.0004VB
VA=0.01VB
Bernoulli's equation relates the pressure and velocity at two points along the streamline:
PA+12ρV2A=PB+12ρV2B
PB−PA=12ρ(V2A−V2B)
Substituting the known values:
20=12(1.00×103)(V2A−V2B)
Using VA=0.01VB:
20=12(1.00×103)((0.01VB)2−V2B)
20=12(1.00×103)(0.0001V2B−V2B)
20=12(1.00×103)(−0.9999V2B)
20=−499.95V2B
V2B=−20−499.95≈0.04001
VB≈√0.04001≈0.200m/s
Using VA=0.01VB:
VA=0.01×0.200≈0.002m/s
Using the formula for volume flow rate:
Q=ABVB
Substituting the values:
Q=0.0004π×0.200
Q≈0.0004×3.1416×0.200≈0.000251m3/s
The rate of flow of liquid through the pipe is approximately:
Q≈2.51×10−4m3/s
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Very Short Answer Questions)54videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Additional Questions)3videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Short Answer Type Questions)5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
Similar Questions
In the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
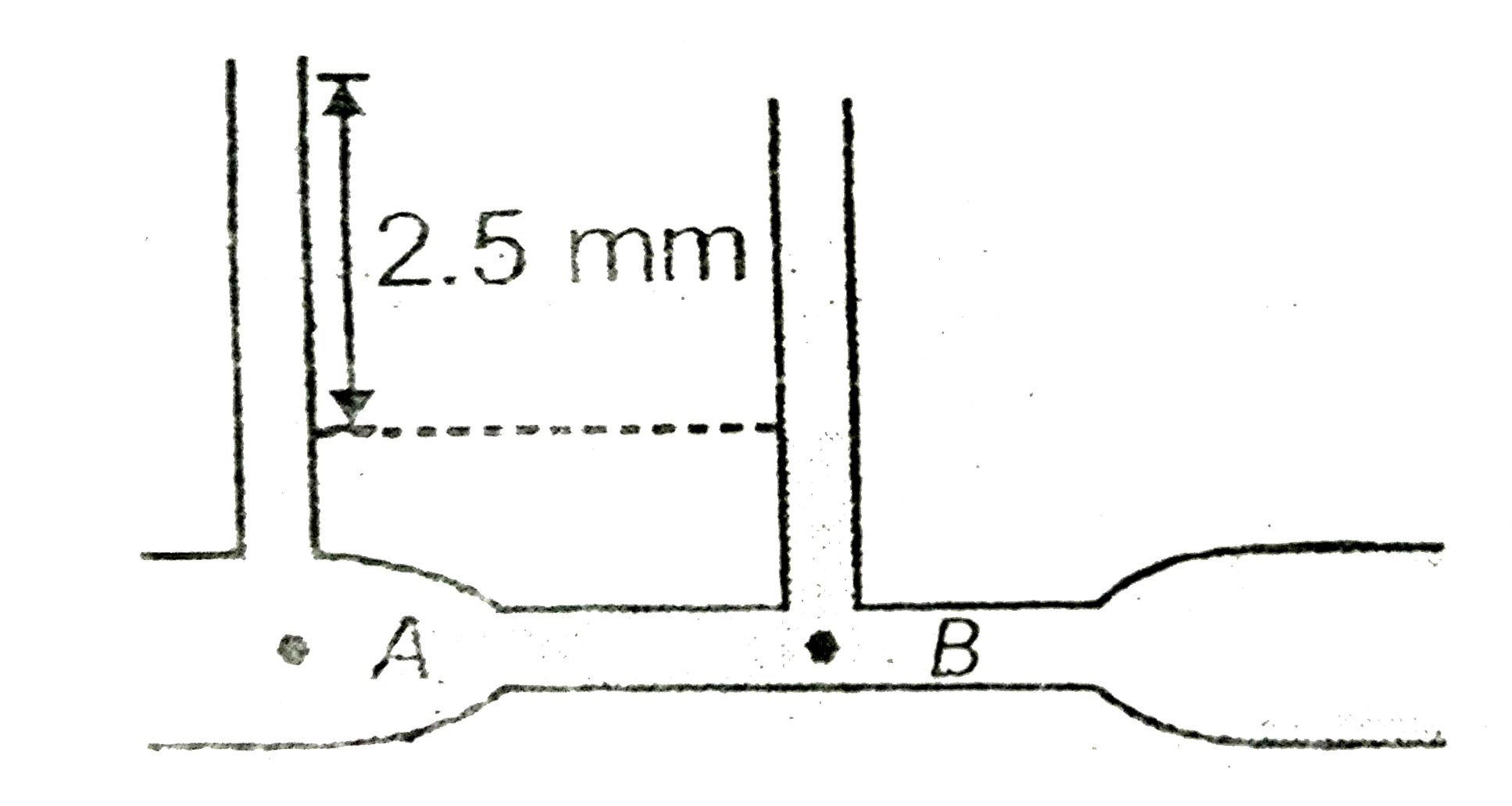 View Solution
View SolutionA steel ball of density 8.0×103kg/m3 and radius 2 mm is observed to fall with a terminal velocity 1.0×10−2m/s in a liquid of density 1.8×103kg/m3 . Calculate the viscosity of the liquid.
View Solution
Knowledge Check
- Question 1 - Select One
In a horizontal pipeline of uniform cross section the pressure falls by 8N/m2 between two points separated by 1km. If oil of density 800kg/m3 flows through the pipe, find the change in KE per kg of oil at these points.
A10−2J/kgB10−3J/kgC10−4J/kgD10−1J/kg - Question 2 - Select One
The workdone by pressure in forcing 1m3 of water through a pipe if the pressure difference across the pipe is 104 Pa, is
A105JB104JC103JD102J
A pipe of circular cross-section of inner radius r and outer radius 2r is bent into a semi circle as shown in the diagram. A fluid of density ρ=103kg/m3 is flowing through it. The breaking stress of the material of the pipe is 3×107n/m2. The maximum velocity with which the fluid can flow in the pipe is k×100m/s. find value of k.
 View Solution
View SolutionWater flows in a horizontal pipe whose one end is closed with a value and the pressure gauge falls to 1×105N/m2 when the value is opend. Calculate the speed of water flowing in the pipe.
View SolutionWater is flowing through a horizontal pipe whose one end is closed with a valve. Initially the pressure recorded by pressure gauge ia 4×105N/m2. On opening the valve, the pressure gauge records 2×105N/m. Find the speed of water flowing through the pipe.
View Solution1.The ratio of diameters at two poits of a pipe are 2 : 1 then what will be ratio of velocity of liquid flow through there points?
View SolutionThe speed of a liquid flowing through a pipe increases and its pressure decreases when liquid passes through a narrow constriction in the pipe. Why?
View SolutionThe diameters of open and narrow ends of a pipe connected to a venturi-meter is 20 cm and 15 cm, respectively. If the difference of pressure at the ends is 25 cm of Hg, then calculate the volume of water flowing through the pipe per second.
View Solution

