A body is under the action of two equal and oppositely directed forces and the body is rotating with constant non-zero angular acceleration. Which of the following cannot be the separation between the lines of action of the forces ?
1 m
0.4 m
0.25 m
zero
The correct Answer is:D
To solve the problem, we need to analyze the situation where a body is subjected to two equal and opposite forces while rotating with a constant non-zero angular acceleration.
1. Understanding Forces: We have two equal and opposite forces acting on the body. Let's denote these forces as F1 and F2. Since they are equal and opposite, they will not cause any translational motion, but they can create a torque about the center of mass of the body.
2. Torque Calculation: The torque (τ) produced by a force is given by the formula:
τ=r×F
where r is the distance from the pivot point (or center of mass) to the line of action of the force, and F is the magnitude of the force.
3. Condition for Angular Acceleration: For the body to have a constant non-zero angular acceleration, there must be a net torque acting on it. This means that the distance r (the separation between the lines of action of the two forces) must be non-zero.
4. Analyzing the Options:
- If the separation r=0, then both forces act along the same line, and the torque produced by each force will cancel each other out, resulting in a net torque of zero. This would mean that there is no angular acceleration, which contradicts the given condition of constant non-zero angular acceleration.
- Therefore, the separation cannot be zero.
5. Conclusion: The only scenario that cannot occur while the body is rotating with a constant non-zero angular acceleration is when the separation between the lines of action of the forces is zero. Thus, the answer to the question is that the separation cannot be 0.
Final Answer:
The separation between the lines of action of the forces cannot be 0.
τ=r×F
where r is the distance from the pivot point (or center of mass) to the line of action of the force, and F is the magnitude of the force.
- If the separation r=0, then both forces act along the same line, and the torque produced by each force will cancel each other out, resulting in a net torque of zero. This would mean that there is no angular acceleration, which contradicts the given condition of constant non-zero angular acceleration.
- Therefore, the separation cannot be zero.
The separation between the lines of action of the forces cannot be 0.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Knowledge Check
A body is acted upon by two unequal forces in opposite directions, but not in the same line. The effect is that:
A(a) the body will only have rotation motionB(b) the body will only have translational motionC(c) the body will have neither rotational motion nor translational motionD(d) the body will have rotational as well as translational motionA body is falling freely under the action of gravity alone in vacuum. Which of the following quantities remain constant during the fall ?
AKinetic energyBPotential energyCTotal mechanical energyDTotal linear momentum
A body is under the action of two mutually perpendicular forces of 3 N and 4 N. The resultant force acting on the body is
View SolutionA body is under the action of two mutually perpendicular forces of 3 N and 4 N. The resultant force acting on the body is
View SolutionFor a body to be in equilibrium under the combined action of several forces
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
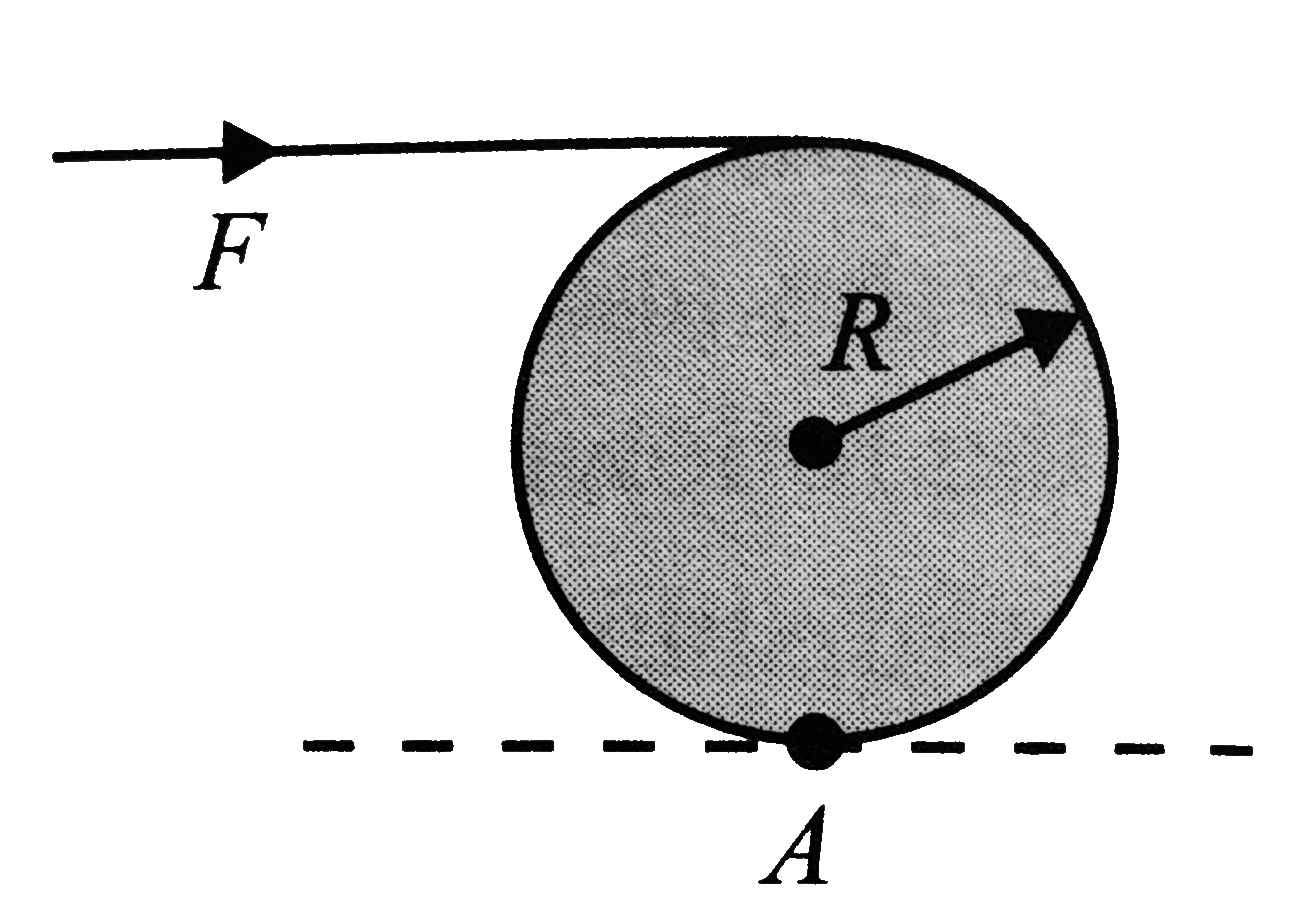
Component of reaction at the hinge in the horizontal direction is
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
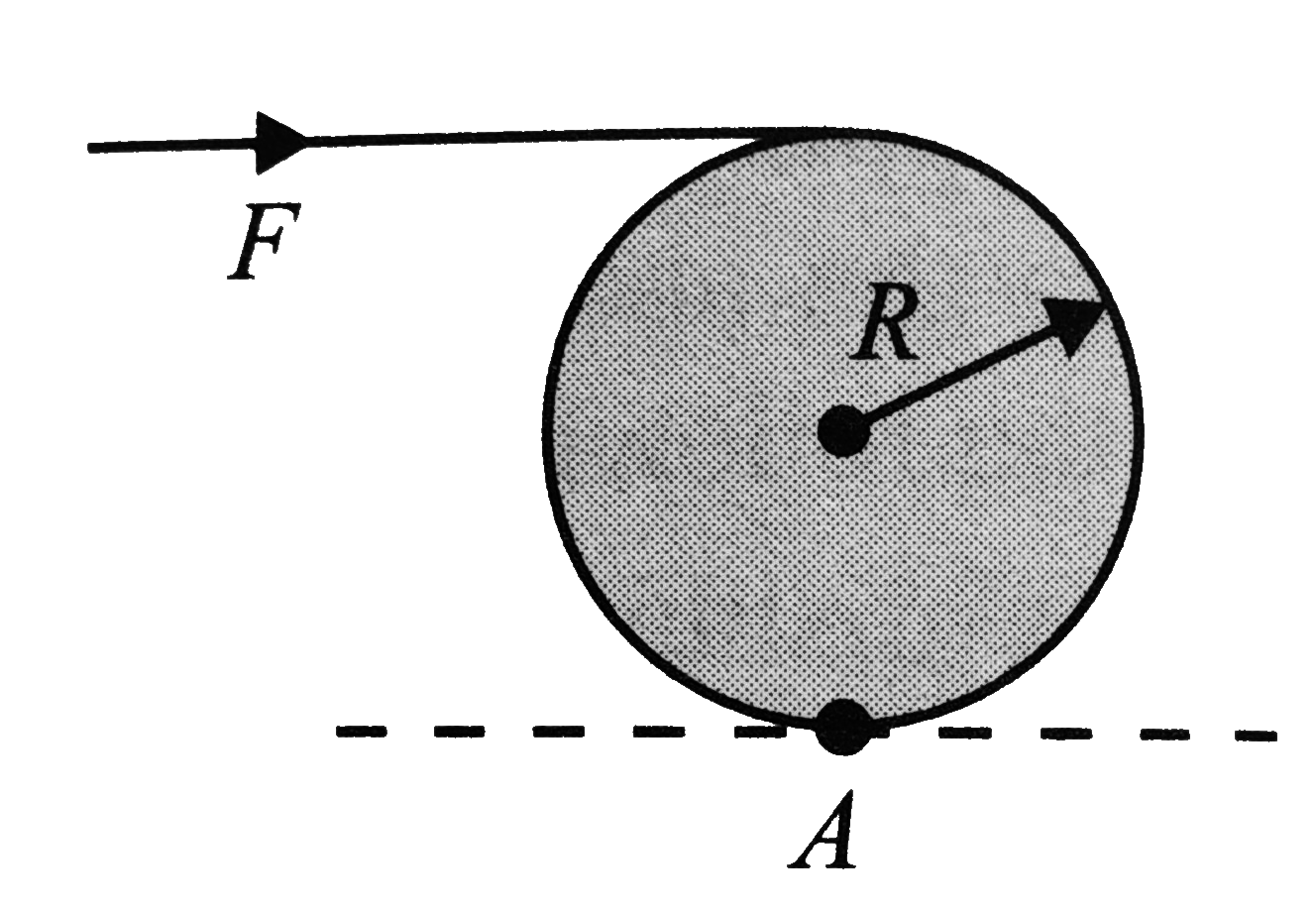
Component of reaction at the hinge in the vertical direction is
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
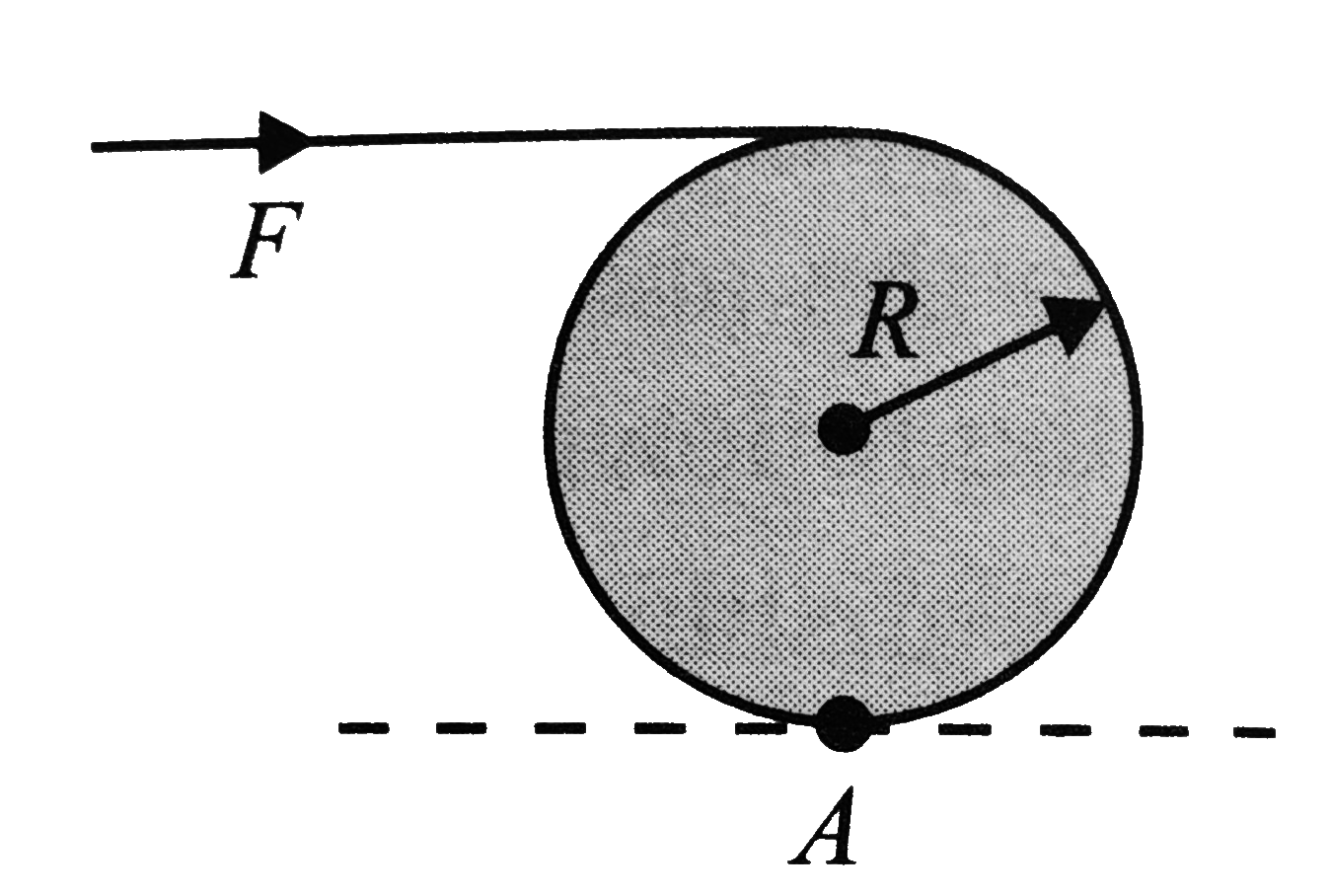
Tangential acceleration of the centre of mass is
View Solution
