A body of mass 4 kg is moving with momentum of 8kgms−1. A force of 0.2 N acts on it in the direction of motion of the body for 10 s. The increase in kinetic energy is
10 J
8.5 J
4.5 J
4 J
The correct Answer is:C
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the initial velocity (u) of the body
The momentum (P) of the body is given by the formula:
P=m⋅u
Where:
- P=8kg m/s
- m=4kg
Rearranging the formula to find the initial velocity (u):
u=Pm=8kg m/s4kg=2m/s
Step 2: Calculate the acceleration (a) caused by the force
The force (F) acting on the body is given as:
F=0.2N
Using Newton's second law:
a=Fm=0.2N4kg=0.05m/s2
Step 3: Calculate the final velocity (v) after 10 seconds
Using the formula for final velocity:
v=u+a⋅t
Where:
- t=10s
Substituting the values:
v=2m/s+(0.05m/s2⋅10s)
v=2m/s+0.5m/s=2.5m/s
Step 4: Calculate the initial kinetic energy (KE_initial)
The initial kinetic energy (KE_initial) can be calculated using the formula:
KE=12mu2
Substituting the values:
KEinitial=12⋅4kg⋅(2m/s)2
KEinitial=12⋅4⋅4=8J
Step 5: Calculate the final kinetic energy (KE_final)
The final kinetic energy (KE_final) can be calculated using the formula:
KE=12mv2
Substituting the values:
KEfinal=12⋅4kg⋅(2.5m/s)2
KEfinal=12⋅4⋅6.25=12.5J
Step 6: Calculate the increase in kinetic energy
The increase in kinetic energy (ΔKE) is given by:
ΔKE=KEfinal−KEinitial
ΔKE=12.5J−8J=4.5J
Final Answer
The increase in kinetic energy is 4.5J.
---
The momentum (P) of the body is given by the formula:
P=m⋅u
Where:
- P=8kg m/s
- m=4kg
u=Pm=8kg m/s4kg=2m/s
The force (F) acting on the body is given as:
F=0.2N
a=Fm=0.2N4kg=0.05m/s2
Using the formula for final velocity:
v=u+a⋅t
Where:
- t=10s
v=2m/s+(0.05m/s2⋅10s)
v=2m/s+0.5m/s=2.5m/s
The initial kinetic energy (KE_initial) can be calculated using the formula:
KE=12mu2
KEinitial=12⋅4kg⋅(2m/s)2
KEinitial=12⋅4⋅4=8J
The final kinetic energy (KE_final) can be calculated using the formula:
KE=12mv2
KEfinal=12⋅4kg⋅(2.5m/s)2
KEfinal=12⋅4⋅6.25=12.5J
The increase in kinetic energy (ΔKE) is given by:
ΔKE=KEfinal−KEinitial
ΔKE=12.5J−8J=4.5J
The increase in kinetic energy is 4.5J.
Topper's Solved these Questions
Similar Questions
The initial speed of a body of mass 2kg is 5ms−1 A force acts for 4 seconds in the direction of motion of the body. The force time graph is shown in Calculate impulse of the force and also find the speed of the body .
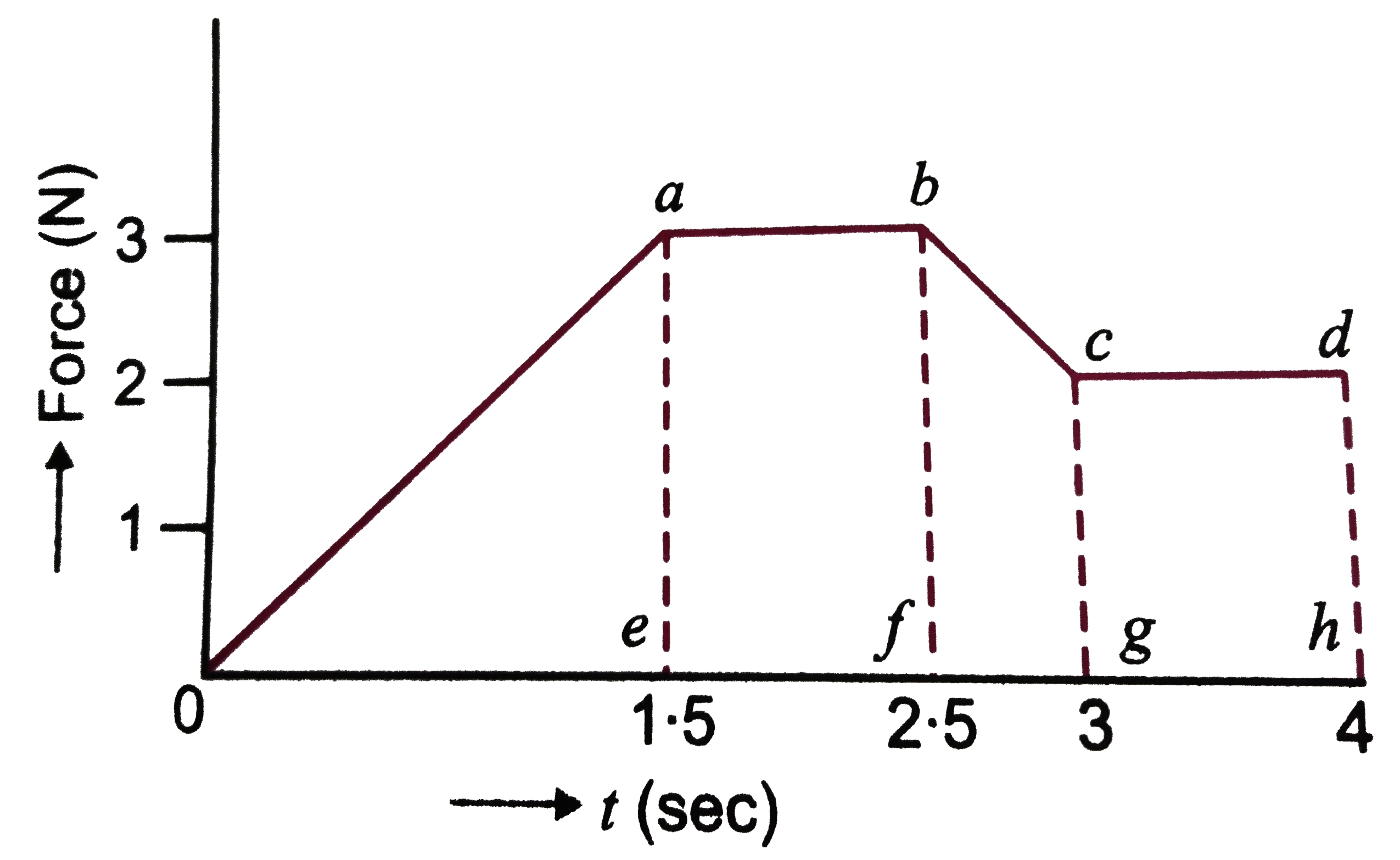 .
.
View SolutionA body of mass5kg is moving with a momentum of 10kgm/s. A force of 0.2N acts on it in the direction of motion of the body for 10sec. The increase in its kinetic energy.
View Solution
Knowledge Check
A body of mass 5 kg is moving with a momentum of 10kgms−1. A force of 0.2 N acts on it in the direction of motion of body for 10 s. The increase in its kinetic energy is
A2.8 JB3.2 JC3.8 JD4.4 JA bodu of mass 4kg is moving with momentant of 8kgms−1 A force of 0.2N acts on it in the direction of motion of the body for 10s The increases in kinetic energy is
A10JB0.5JC4.5JD4JA body of mass5kg is moving with a momentum of 10kgm/s. A force of 0.2N acts on it in the direction of motion of the body for 10sec. The increase in its kinetic energy.
A2.8JB3.2JC3.8JD4.4J
The momentum of a body of mass 8 kg is 20 kg m/s. A force of 12 N acts on the body in the direction of motion for 4 s, the increase in the kinetic energy is
View SolutionA body of mass 8 kg is moving with a velocity of 4 m/s, find its momentum.
View SolutionA body of mass 2kg is moving along north-east direction with a speed √2 m/s. A force of 0.2N is applied on the body due west for 10 sec. The final velocity ofthe body is :
View SolutionA body of mass 1kg is moving with a uniform speed of 1m/s in a circular path of radius 1m. The external force acting on the body is
View SolutionA constant force acting on a body of mass of 5 kg change its speed from 5ms−1 to 10ms−1 in 10s without changing the direction of motion. The force acting on the body is
View Solution
