A constant force acting on a body of mass of 5 kg change its speed from to in without changing the direction of motion. The force acting on the body is
A
1.5N
B
2N
C
2.5N
D
5N
Video Solution
Text Solution
The correct Answer is:C
Here, 5kg, u= using v=u+at
As, F=ma
|
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Newton'S Third Law Of Motion
15 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Conservation Of Momentum
4 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Newton'S First Law Of Motion
2 Videos
- KINETIC THEORYBOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
Question stimulus:-
A constant force acting on a body of mass 5 kg changes its speed from 2ms−1 to 4ms−1 in 20 s, without changing its direction of motion. The magnitude of the force isA0.2 NB0.5 NC2 ND5 NA constant force acting on a body of mass 5kg change its speed from 5ms−1 in 10s without changing the direction of motion. The force acting on the body is
A1.5NB2NC2.5ND5NWhat force should be applied on a body of mass 500 kg to change its velocity from 4 ms1 to 6 ms−1 in one second ?
A250 NB500 NC1000 ND2000 N
Calculate the net force acting on a body of mass 10 kg moving with a unifrom velocity of 2ms−1 .
View SolutionA body of mas 2kg has an initial speed 5ms−1 A force acts on it for some time in the direction of motion The force-time graph is shown. Find the final speed of the body
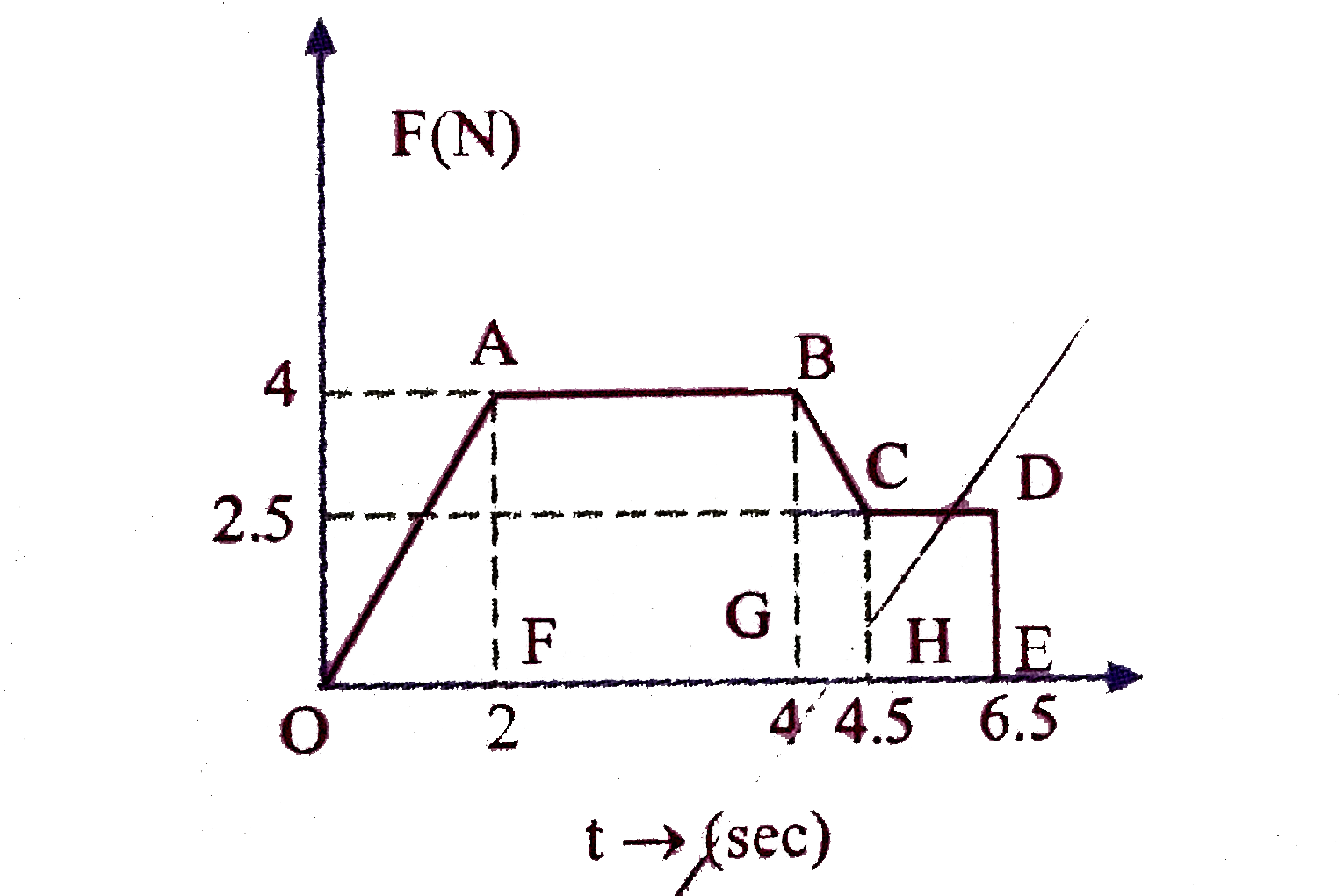 .
.
View SolutionCertain force acting on a 20 kg mass changes its velocity from 5ms−1 to 2ms−1. Calculate the work done by the force.
View SolutionWhat force will change the velocity of a body of mass 1 kg from 20ms−1to 30ms−1 in two seconds?
View SolutionThe average resisting force that must act on 5kg mass to reduce its speed from 65 to 15ms−1 in 2s is
View Solution
