A body of mass m attached to one end of an ideal spring of force constant k is executing simple harmonic motion. Establish that the time - period of oscillation is T=2π√m/k.
Derivation : Consider a body of mass m attached to one end B of a light elastic massless apring of spring constant k. The other end A of the spring is fixed to a rigid support. The body is resting on frictionless horizontal surface. The weight of body is balanced by the reaction of the horizontal surface.

Let the body be displaced towards right through a small distance y. The spring gets stretched. A restoring force F comes into play due to elastic nature of the spring.
F=−ky
In the displaced position if the body is left free.
It will start executing SHM on the smooth surface.
Here, inertia factor = mass of body (m)
Spring factor = force constant of spring = k
∴ Periodic Time, T=2π√Inertia factorSpring factor
=2π√mk
T=2π√mk
Topper's Solved these Questions
- SAMPLE QUESTION PAPER 5BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 5EXERCISE - SECTION - D (Answer all questions.)
6 Videos
- SAMPLE QUESTION PAPER 5BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 5EXERCISE - SECTION - B (Answer all questions.)
13 Videos
- SAMPLE QUESTION PAPER 4BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 4EXERCISE - SECTION - D (Answer all questions.)
7 Videos
- SAMPLE QUESTION PAPER-2 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-2 EXERCISE - SECTION-D
10 Videos
Similar Questions
A spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionA particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
View Solution
Knowledge Check
A body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of (5/π) Hz. The value of spring constant is
A4Nm−1B3Nm−1C2Nm−1D5Nm−1The displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2πA particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2
A block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is
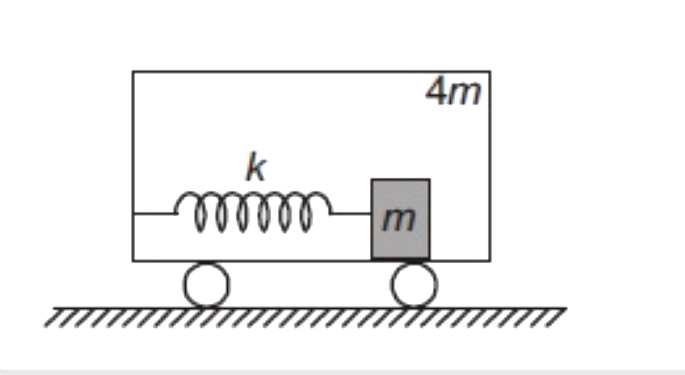
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA body of mass m suspended from an ideal spring is executing simple harmonic oscillations. The force constant of the spring is k and the time period of the body is T. Show by dimensional method that the formula T=2πm/k is incorrect. Establish its correct form.
View SolutionA solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.

View SolutionA body of mass m hung at one end of the spring executes simple harmonic motion . The force constant of a spring is k while its period of vibration is T. Prove by dimensional method that the equation T=2π√m/k is correct. Dervive the correct equation , assuming that they are related by a power law.
View Solution
