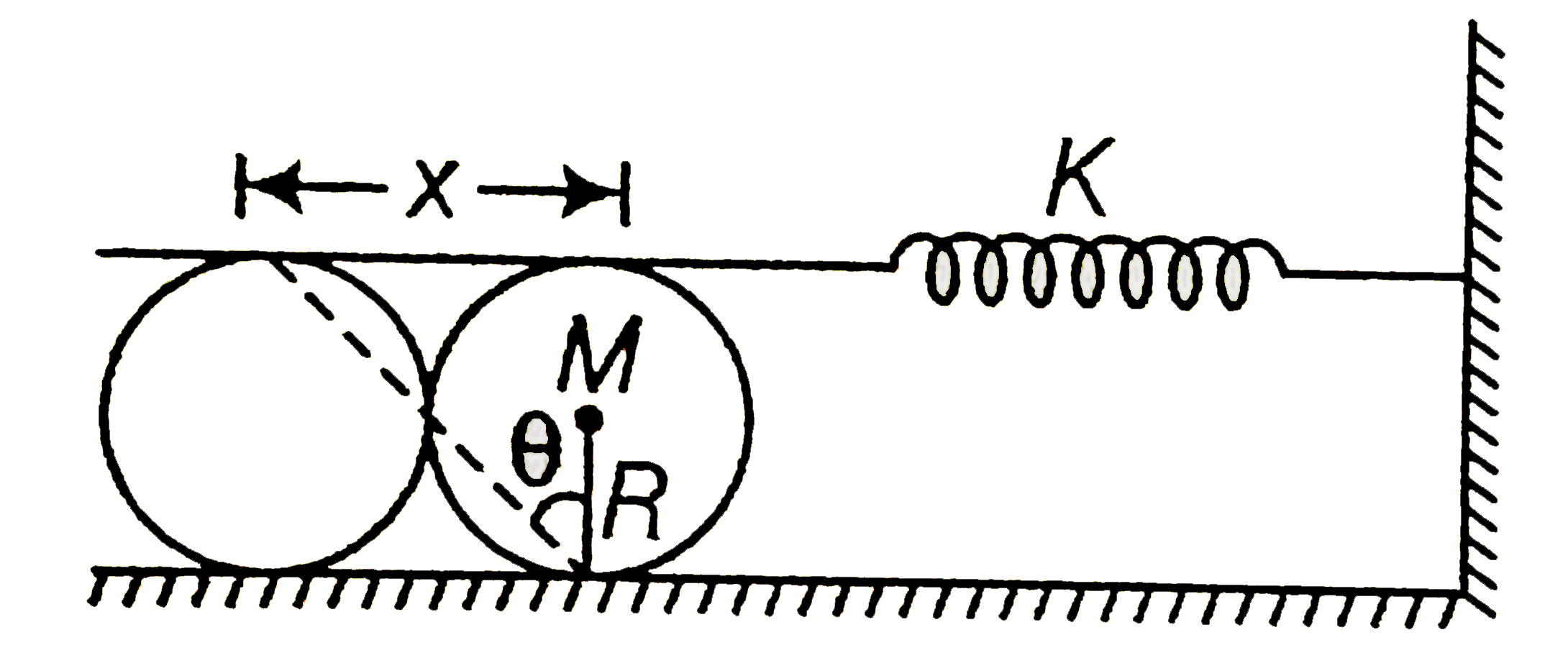
A solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.
(a)2π√M2k
(b)π√3M2k
(c)π√2M3k
(d)2π√7M5k
The correct Answer is:D
About the point of contact,τ=(kx)R⇒c=kR and I=32mR2
⇒T=2π√Ic=2π√3/2mR2kR=2π√3m2k
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)40videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question56videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE2videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
Similar Questions
A solid cylinder of mass m is attached to a horizontal spring with force constant k. The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period T=2π√3m2k, if displaced from mean position.
View SolutionA solid cylinder attached to horizontal massless spring can roll without slipping along a horizontal surface. Find time period of oscillation.
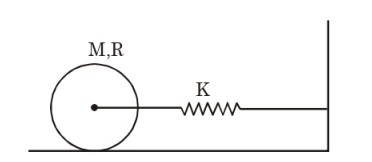View SolutionA spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
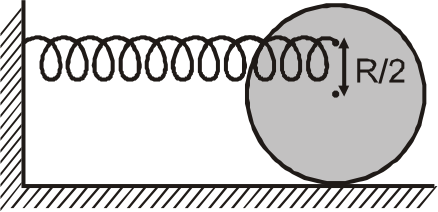View SolutionA solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png)
View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is
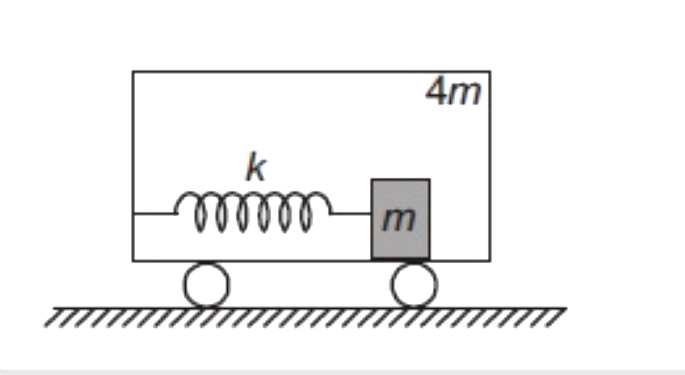View SolutionA mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?
View SolutionA solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
View SolutionA solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
View SolutionA solid cylinder is attached to a horizonatal massless spring as shwn in figure.If the cyclinder rolls without slipping, the time period of oscillation of the cyclinder is
View Solution