A body of mass m dropped from a certain height strikes a light vertical fixed spring of stifness k. the height of its fall before touching the spring the if the maximum compression of the spring the equal to 3mgk is
3mg2k
2mgk
3mg4k
mg4k
The correct Answer is:A
To solve the problem, we need to analyze the energy transformations that occur when a body of mass m is dropped from a height h and strikes a vertical spring with spring constant k. The maximum compression of the spring is given as 3mgk.
1. Identify the Energy Types:
- When the body is dropped from height h, it has gravitational potential energy which converts into kinetic energy as it falls and then into elastic potential energy when it compresses the spring.
2. Potential Energy at Height h:
- The gravitational potential energy (PE) of the body at height h is given by:
PE=mgh
3. Maximum Compression of the Spring:
- When the body compresses the spring to its maximum compression x, the potential energy stored in the spring is given by:
PEspring=12kx2
4. Energy Conservation Principle:
- At the point of maximum compression, all the gravitational potential energy is converted into the elastic potential energy of the spring. Thus, we can write:
mgh=12kx2
5. Substituting for x:
- We know from the problem that the maximum compression x is given as 3mgk. Substituting this into the energy conservation equation:
mgh=12k(3mgk)2
6. Simplifying the Equation:
- Substitute x into the equation:
mgh=12k⋅9m2g2k2
- This simplifies to:
mgh=9mg22k
7. Solving for h:
- Rearranging the equation to solve for h:
h=9g2k
8. Final Result:
- Thus, the height h from which the body is dropped is:
h=9mg2k
Conclusion:
The height h from which the body is dropped before touching the spring is 9mg2k.
- When the body is dropped from height h, it has gravitational potential energy which converts into kinetic energy as it falls and then into elastic potential energy when it compresses the spring.
- The gravitational potential energy (PE) of the body at height h is given by:
PE=mgh
- When the body compresses the spring to its maximum compression x, the potential energy stored in the spring is given by:
PEspring=12kx2
- At the point of maximum compression, all the gravitational potential energy is converted into the elastic potential energy of the spring. Thus, we can write:
mgh=12kx2
- We know from the problem that the maximum compression x is given as 3mgk. Substituting this into the energy conservation equation:
mgh=12k(3mgk)2
- Substitute x into the equation:
mgh=12k⋅9m2g2k2
- This simplifies to:
mgh=9mg22k
- Rearranging the equation to solve for h:
h=9g2k
- Thus, the height h from which the body is dropped is:
h=9mg2k
The height h from which the body is dropped before touching the spring is 9mg2k.
Topper's Solved these Questions
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:A Only One Option is Correct
Explore 42 Videos
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:B More than One Option is Correct
Explore 26 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
A block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
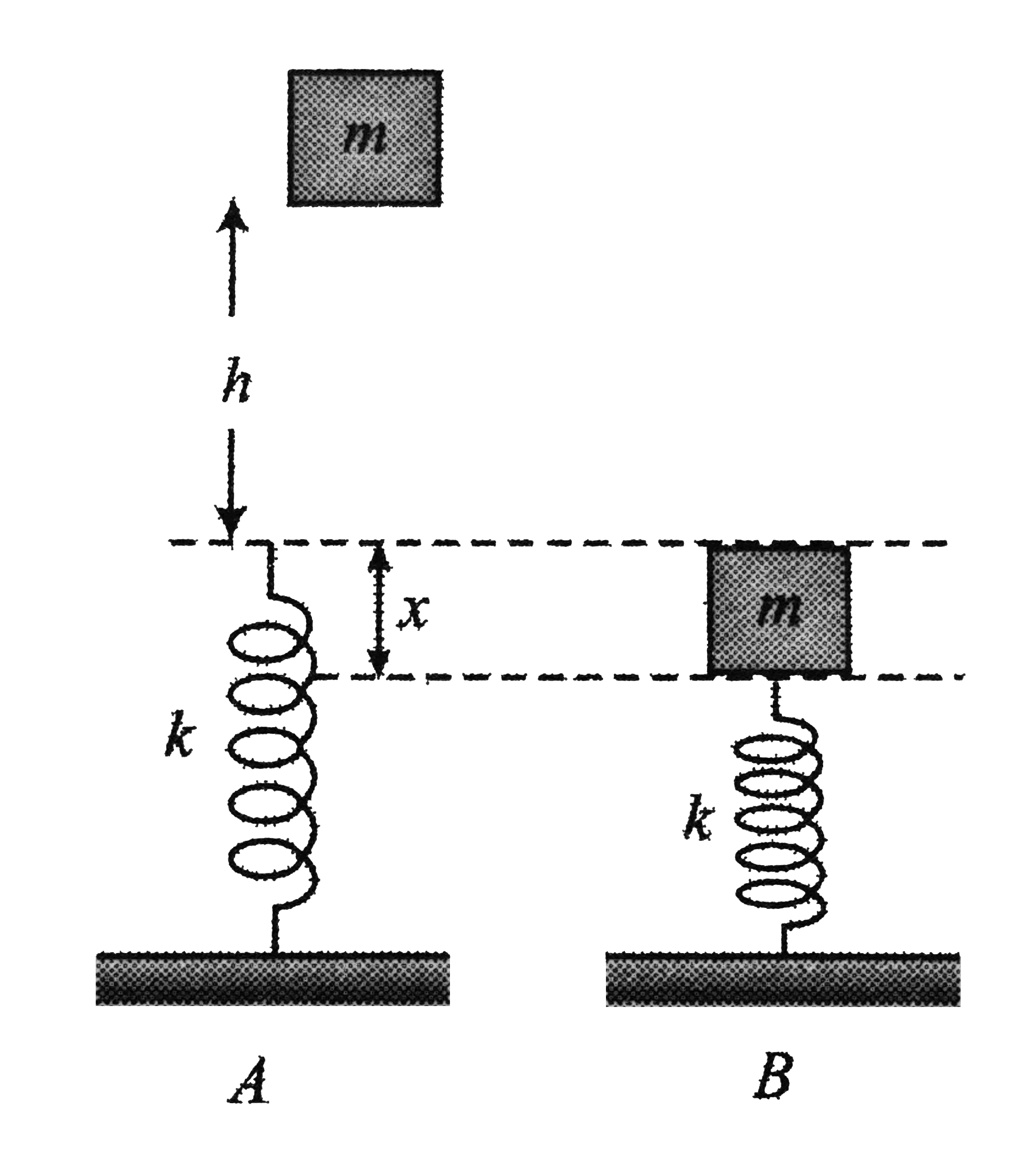
View SolutionA block of mass m is slowly lowered from a point where it just touches a vertical fixed spring of stiffness k, till it remains stationary after the applied force is withdrawn. Find the work done by the external agent(a) in compressing the spring by a distance x and (b) bringing the block to its stable equilibrium position.

View SolutionA block of mass m is moving with an initial velocity v0 towards a stationary spring of stiffness k attached to the wall as shown in figure

a. Find the maximum compression in the spring.
b. Is the work done by the spring negative or positive?
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionA 20 kg body is released from rest so as to slide in between vertical rails and compresses a vertical spring (k=1920Nm) placed at a distance h=1.0m from the strating position of the body. The rails offer a frictional force of 40 N opposing the motion of body. Find (a) the velocity v of the body just before striking with the spring, (b) the maximum compression of the spring and (c ) the distance h′ through which the body is rebounded up.
View SolutionA sphere of mass m and radius R rolls without sliding on a horizontal surface. It collides with a light spring of stiffness K with a kinetic energy E. If the surface (AB) under the spring is smooth, find the maximum compression of the spring.
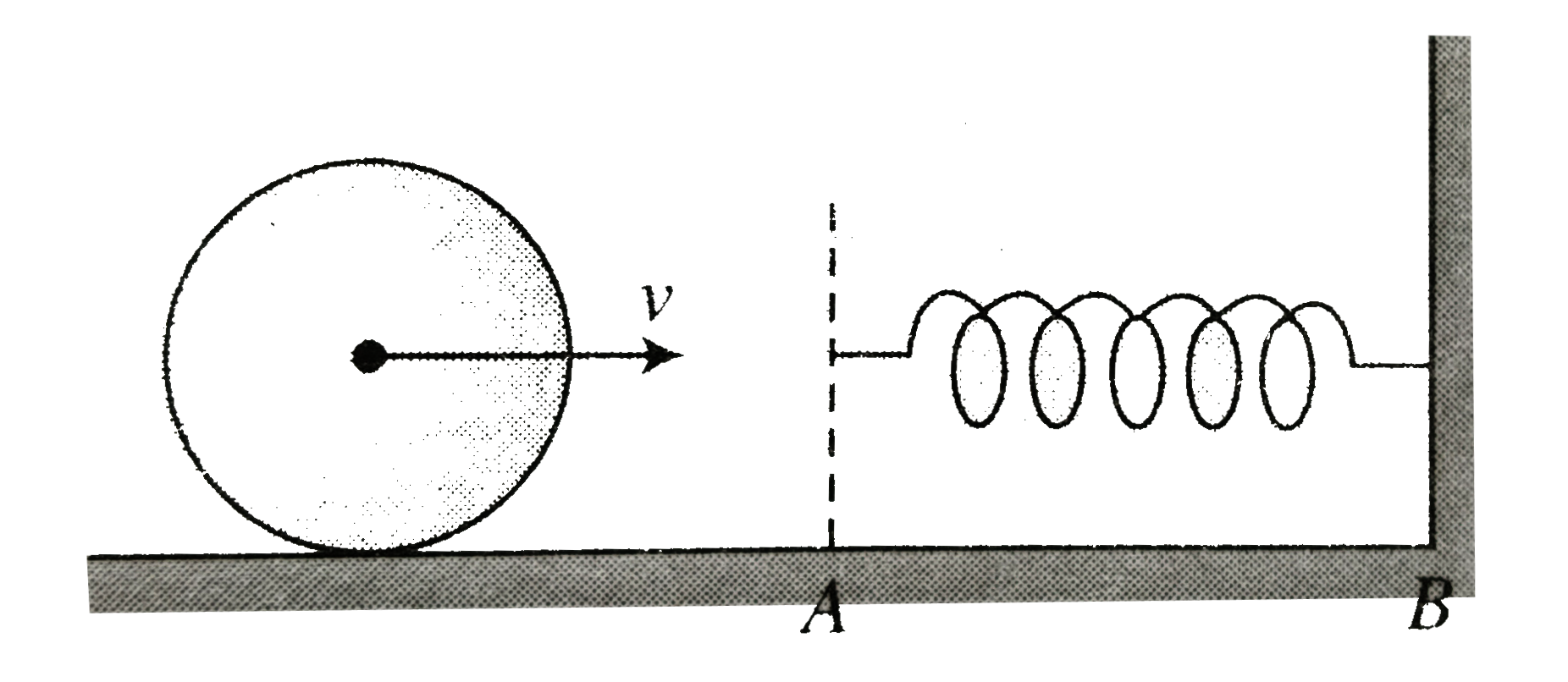
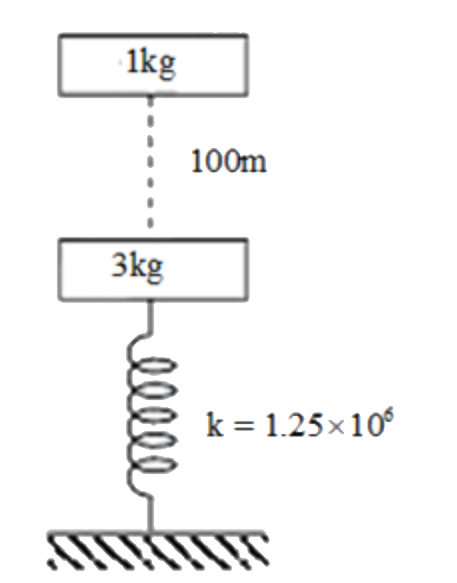
View SolutionA block of mass 1kg is dropped on a spring - mass system as shown in the figure. The block traves 100 meters in the air before strinking the 3 kg mass. Calculate maximum compression in the spring, if both the blocks move together after the collision. Spring constant of the string k=1.25×106.
View SolutionA ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View Solution
