Question

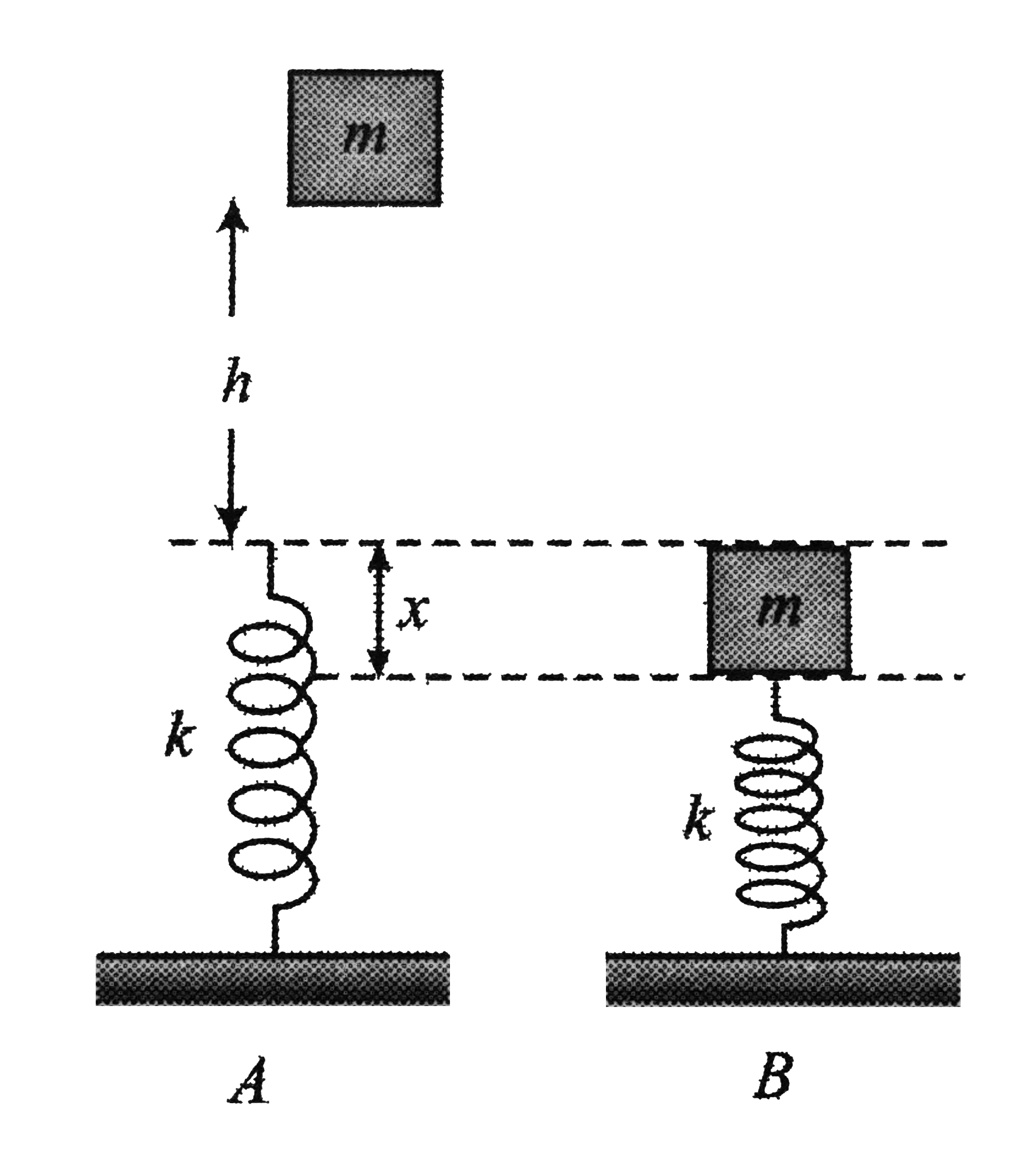
A 20 kg body is released from rest so as to slide in between vertical rails and compresses a vertical spring $(k=1920\frac{N}{m}$) placed at a distance $h=1.0$m from the strating position of the body. The rails offer a frictional force of 40 N opposing the motion of body. Find (a) the velocity v of the body just before striking with the spring, (b) the maximum compression of the spring and (c ) the distance $h^{\prime }$ through which the body is rebounded up.

Explanation

To solve the problem step by step, we will break it down into three parts as requested.

Given Data:
- Mass of the body, $$m=20\text{kg}$$
- Spring constant, $$k=1920\text{N/m}$$
- Distance from the starting position to the spring, $$h=1.0\text{m}$$
- Frictional force, $$f=40\text{N}$$
- Acceleration due to gravity, $$g=10{\text{m/s}}^2$$

Part (a): Find the velocity $$v$$ of the body just before striking the spring.

1. Calculate the potential energy lost by the body:
\( \text{Potential Energy (PE)} = mgh = 20 \times 10 \times 1 = 200 \, \text{J} \)

2. Calculate the work done against friction:
\( \text{Work done against friction} = f \cdot h = 40 \times 1 = 40 \, \text{J} \)

3. Apply the work-energy principle:
The loss in potential energy equals the gain in kinetic energy plus the work done against friction:
\( mgh = \frac{1}{2} mv^2 + f \cdot h \)
Substituting the known values:
\( 200 = \frac{1}{2} \cdot 20 \cdot v^2 + 40 \)

4. Rearranging the equation:
\( 200 - 40 = 10v^2 \)
\( 160 = 10v^2 \)
\( v^2 = \frac{160}{10} = 16 \)
\( v = \sqrt{16} = 4 \, \text{m/s} \)

Part (b): Find the maximum compression of the spring.

1. Use the conservation of energy between the point just before striking the spring and the maximum compression of the spring:
\( \text{Loss in PE} + \text{KE} = \text{Spring Potential Energy} + \text{Work done against friction} \)
\( mgh + \frac{1}{2} mv^2 = \frac{1}{2} kx^2 + f \cdot x \)

2. Substituting the known values:
\( 200 + \frac{1}{2} \cdot 20 \cdot 4^2 = \frac{1}{2} \cdot 1920 \cdot x^2 + 40x \)
\( 200 + 160 = 960x^2 + 40x \)
\( 360 = 960x^2 + 40x \)

3. Rearranging the equation:
\( 960x^2 + 40x - 360 = 0 \)

4. Dividing the entire equation by 40 for simplification:
\( 24x^2 + x - 9 = 0 \)

5. Using the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \):
\( x = \frac{-1 \pm \sqrt{1^2 - 4 \cdot 24 \cdot (-9)}}{2 \cdot 24} \)
\( x = \frac{-1 \pm \sqrt{1 + 864}}{48} \)
\( x = \frac{-1 \pm 29.39}{48} \)
\( x = \frac{28.39}{48} \approx 0.59 \, \text{m} \)

Part (c): Find the distance \( h' \) through which the body is rebounded up.

1. Using conservation of energy again between maximum compression of the spring and the height reached after rebounding:
\( \frac{1}{2} kx^2 = mgh' + f \cdot h' \)

2. Substituting the known values:
\( \frac{1}{2} \cdot 1920 \cdot (0.59)^2 = 20 \cdot 10 \cdot h' + 40h' \)

3. Calculating the left side:
\( \frac{1}{2} \cdot 1920 \cdot 0.3481 \approx 334.88 \)

4. Setting up the equation:
\( 334.88 = 200h' + 40h' \)
\( 334.88 = 240h' \)
\( h' = \frac{334.88}{240} \approx 1.40 \, \text{m} \)

Summary of Answers:
(a) The velocity \( v \) of the body just before striking the spring is 4 m/s.
(b) The maximum compression of the spring is approximately 0.59 m.
(c) The distance \( h' \) through which the body is rebounded up is approximately 1.40 m.