A body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
θ=tan−1μ
θ=tan−1(1μ)
θ=tan−1(m)μ
θ=tan−1(μ)m
The correct Answer is:A
(d) Consider a body of mass m palced on a rough inclined surface and it is just on the point of sliding down, with coefficient of friction μ inclined at angle θ, as shown in figure.
At the equilibrium point O,
In case of limiting condition, F=mgsinθ......(i)
Normal force, R=mgcosθ...(ii)
Now, comparing Eqs. (i) and (ii), we get
FR=mgsinθmgcosθ(∴ force of friction,F=μR)
μ=tanθ⇒θ=tan−1(μ)
This is maximum value of theta for mass m to be a rest. For samller θ, body will be at rest, i.e., in equilibrium.
So angle of repose, i.e. θ=tan−1μ
Topper's Solved these Questions
Similar Questions
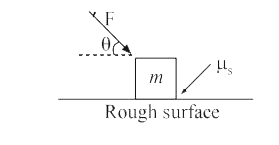
What is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
View SolutionA body of mass M is placed on a rough inclined plane of inclination θ and coefficient of friction μk. A force of (mgsinθ+μkmgcosθ) is applied in the upward direction, the acceleration of the body is
View Solution
Knowledge Check
A body of mass 2 kg is placed on rough horizontal plane. The coefficient of friction between body and plane is 0.2 Then,
 Abody will move in forward direction if F = 5 NBbody will be move in backward direction with acceleration 0.5m/s2 if force F = 3NCif F = 3N, then body will be in rest conditionDBoth a and c are correct
Abody will move in forward direction if F = 5 NBbody will be move in backward direction with acceleration 0.5m/s2 if force F = 3NCif F = 3N, then body will be in rest conditionDBoth a and c are correct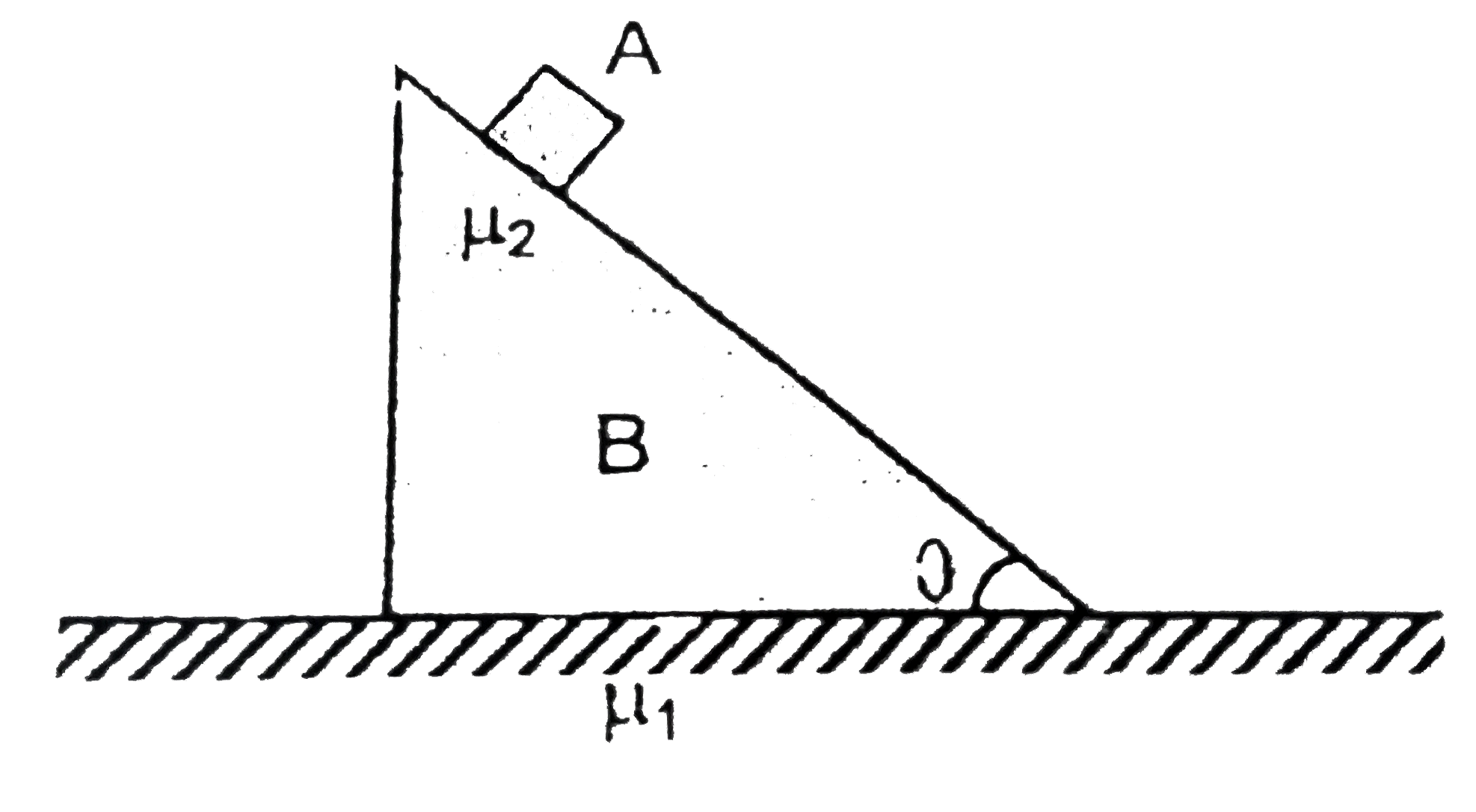
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium ifAμ1=0.1Bμ1=0.2Cμ1=0.3Dμ1=0.4A block of mass m is pulled on an incline surface having coefficient of friction μ=1& angle of inclination θ=30∘, with the horizontal, such that required external force is minimum. The angle made by this force with the incline is :
A45∘B30∘C75∘D53∘
A block of mass m is attached with a massless spring of force constant K. the block is placed over a rough inclined surface for which the coefficient of friction is μ=34 find the minimum value of M required to move the block up the place. (Neglect mass of string and pulley. Ignore friction in pulley).
 .
.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA body of mass M is placed on a rough inclined plane of inclination θ and coefficient of friction μk A force of (mgsinθ+μkmgcosθ) is applied in the upward direction the acceleration of the body is .
View SolutionA block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
View SolutionA block of mass ''m' is attached with a mass - less spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=3/4. The minimum value of 'M' required so that the block on the inclined plane is at rest (neglect mass of string and pulley).

View Solution
