A body of mass m kept on the floor of a lift moving downwards is pulled horizontally. If μ is the coefficient of friction between the surface in contact, then
frictional resistance offered by the floor is 2 μmg, when lift moves up with a uniform velocity of 5 m/s.
rictional resistance offered by the floor is μumg, when lift moves lift moves up with uniform velocity of 3 m/s.
frictional resistance offered by the floor is 4.8μmg, when lift accelerates down with an acceleration of 4.8m/s2
frictional resistance offered by the floor must lie in the range 0≤f<∞
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on a body of mass m placed on the floor of a lift that is moving downwards. We will consider different scenarios based on the motion of the lift and determine the frictional force in each case.
1. Understanding the Scenario:
- A body of mass m is placed on the floor of a lift.
- The lift is moving downwards, and we need to analyze the frictional force when the body is pulled horizontally.
2. Identify Forces Acting on the Body:
- The weight of the body acting downwards: W=mg.
- The normal force N acting upwards, which will be affected by the acceleration of the lift.
3. Case 1: Lift Moving Down with Uniform Velocity:
- When the lift moves down with uniform velocity, the acceleration a=0.
- The normal force N is equal to the weight of the body:
N=mg
- The maximum frictional force Fr is given by:
Fr=μN=μmg
4. Case 2: Lift Accelerating Downwards:
- When the lift accelerates downwards with acceleration a, the effective weight of the body is reduced.
- The normal force N is given by:
N=mg−ma=m(g−a)
- The frictional force is then:
Fr=μN=μm(g−a)
5. Case 3: Lift Moving Up with Uniform Velocity:
- Similar to the first case, when the lift moves up with uniform velocity, the acceleration a=0.
- The normal force remains:
N=mg
- Thus, the frictional force is:
Fr=μmg
6. Conclusion:
- The frictional force when the lift is moving down with uniform velocity is μmg.
- The frictional force when the lift is accelerating downwards is μm(g−a).
- The frictional force when the lift is moving up with uniform velocity is also μmg.
Summary of Results:
- Frictional Force when Lift Moves Down with Uniform Velocity: Fr=μmg
- Frictional Force when Lift Accelerates Downwards: Fr=μm(g−a)
- Frictional Force when Lift Moves Up with Uniform Velocity: Fr=μmg
- A body of mass m is placed on the floor of a lift.
- The lift is moving downwards, and we need to analyze the frictional force when the body is pulled horizontally.
- The weight of the body acting downwards: W=mg.
- The normal force N acting upwards, which will be affected by the acceleration of the lift.
- When the lift moves down with uniform velocity, the acceleration a=0.
- The normal force N is equal to the weight of the body:
N=mg
- The maximum frictional force Fr is given by:
Fr=μN=μmg
- When the lift accelerates downwards with acceleration a, the effective weight of the body is reduced.
- The normal force N is given by:
N=mg−ma=m(g−a)
- The frictional force is then:
Fr=μN=μm(g−a)
- Similar to the first case, when the lift moves up with uniform velocity, the acceleration a=0.
- The normal force remains:
N=mg
- Thus, the frictional force is:
Fr=μmg
- The frictional force when the lift is moving down with uniform velocity is μmg.
- The frictional force when the lift is accelerating downwards is μm(g−a).
- The frictional force when the lift is moving up with uniform velocity is also μmg.
- Frictional Force when Lift Moves Down with Uniform Velocity: Fr=μmg
- Frictional Force when Lift Accelerates Downwards: Fr=μm(g−a)
- Frictional Force when Lift Moves Up with Uniform Velocity: Fr=μmg
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)4videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)7videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PROBLEMS33videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)3videos
GAUSS' LAW
Similar Questions
A lift is moving downwards. A body of mass 2kg kept on the floor is pulled horizontally and is in motion. If the coefficient of friction between the body and floor is 1/2, find the friction acting on the body if (a) lift is moving with a uniform velocity and (b) lift is moving with acceleration 5m/s2 in the downward direction.
View SolutionA body of mass m is moved up (slowly) the plane of verying slope by a tangential force upto height h. The coefficient of friction between the surface and the block is μ.

Select correct option(s)View Solution
Knowledge Check
- Question 1 - Select One
A lift is moving down with an acceleration equal to the acceleration due to gravity. A body of mass M kept on the floor of the lift is pulled horizontally If the coefficient of friction is μ then the frictional resistance offered by the body is .
AμkMgBMgCZeroDμkMg2 - Question 2 - Select One
A lift is moving down with an acceleration equal to the acceleration due to gravity. A body of mass M kept on the floor of the lift is pulled horizontally. If the coefficient of friction is, then the frictional resistance offered by the body is
AμkMgBMgCZeroDμkMg2 - Question 3 - Select One or More
A body of mass m is moved up (slowly) the plane of verying slope by a tangential force upto height h. The coefficient of friction between the surface and the block is μ.
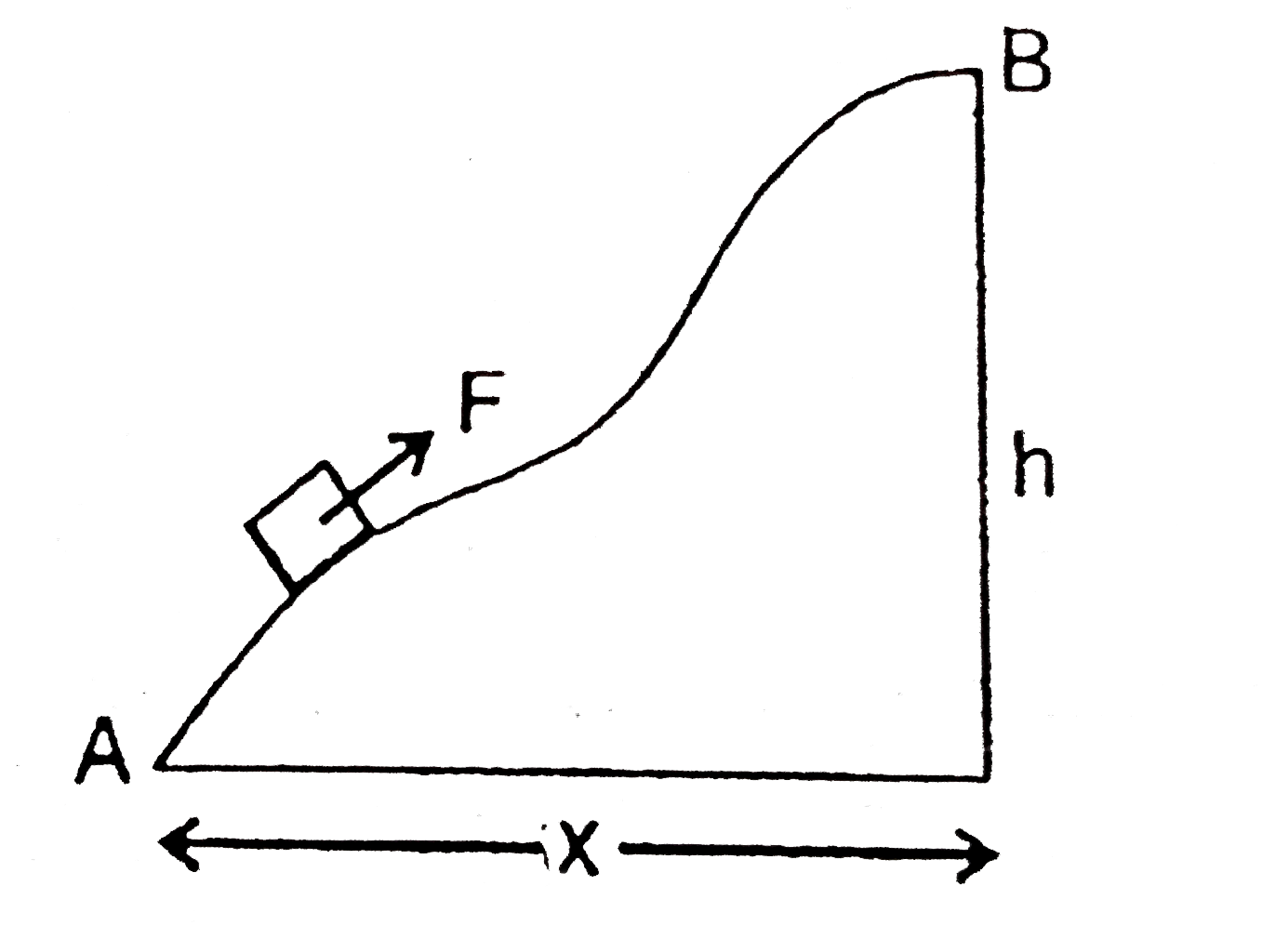
Select correct option(s)AThe work done by gravity on the block from A to B depends upon the height h.BThe work done by gravity on the block from A to B do not depends upon the height h.CTotal work done by all forces on the block from A to B is zeroDFrom A to B work done by friction force on the block is negative.
A block of mass m is kept on an inclined plane of a lift moving down with acceleration of 2m/s2 . What should be the coefficient of friction for the block to move down with constant velocity relative relative to lift?
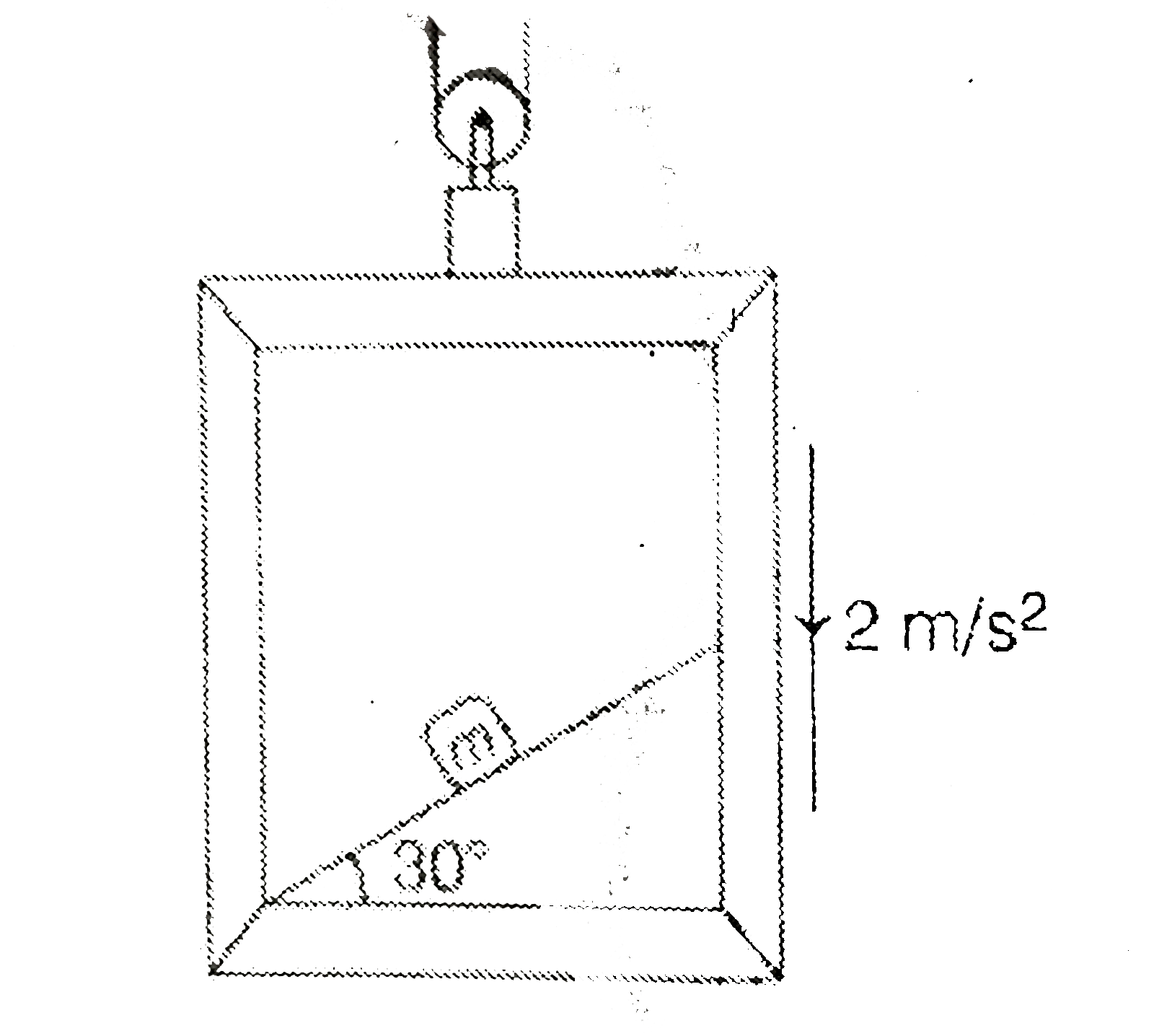 View Solution
View SolutionA block of mass m is kept on an inclined plane of a lift moving down with acceleration of 2ms−1.What should be the coefficient of friction to let the block move down with constant velocity relative to lift.
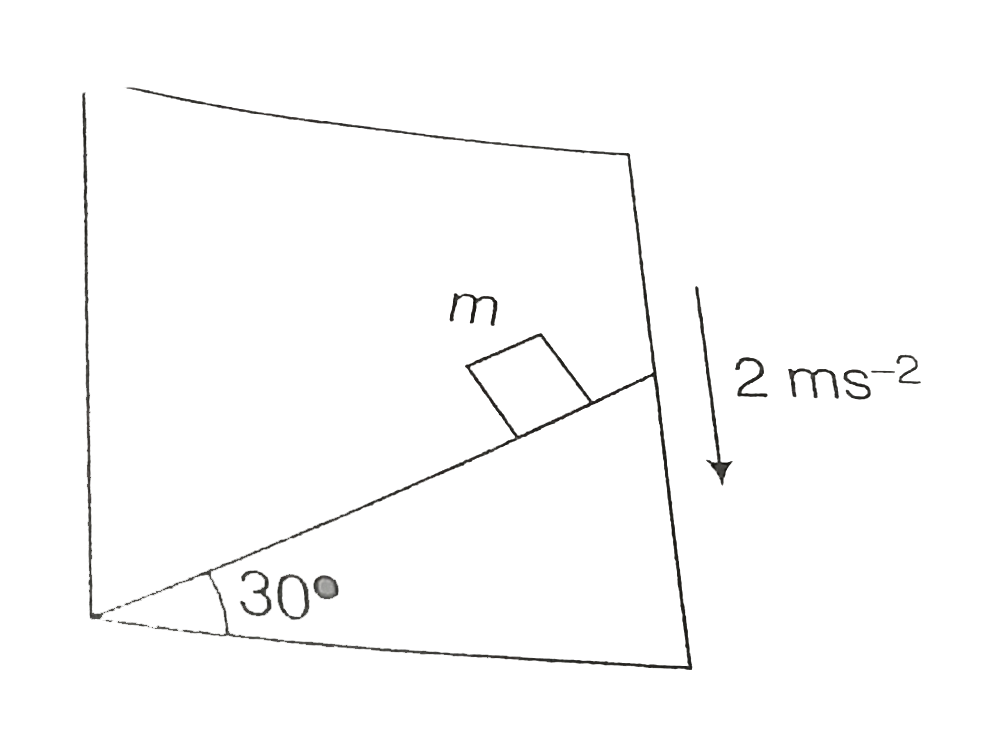 View Solution
View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View SolutionA body of mass M is applying horizontal force to slide a box of mass M1 on a rough horizontal surface The coefficient of friction between the shoe of the boy and the floor is μ and that between the box and the floor is 'μ1' In which of the following cases is it certainly not possible to slide the box ? .
View SolutionA body of mass m, having momentum p, is moving on a rough horizontal surface. If it is stopped in a distance x, the coefficient of friction between the body and the surface is given by
View Solution

