A block of mass m is kept on an inclined plane of a lift moving down with acceleration of 2ms−1.What should be the coefficient of friction to let the block move down with constant velocity relative to lift.
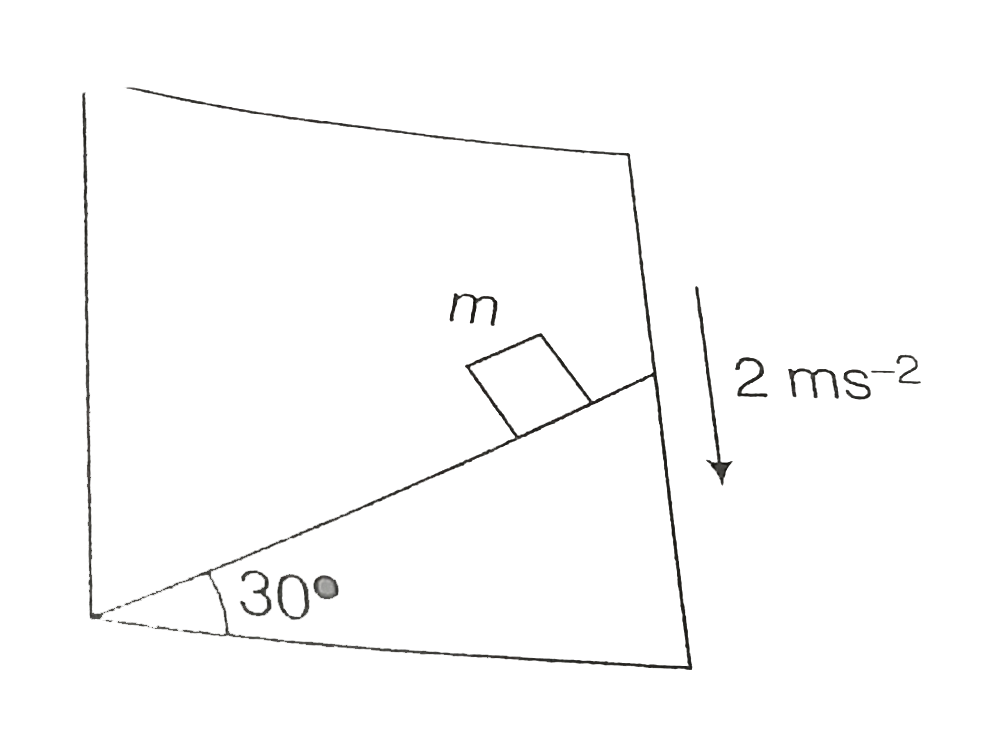
μ=1√3
μ=0.4
μ=0.8
μ=√32
The correct Answer is:A
(a) m(g−a)sinθ=μm(g−a)cosθ
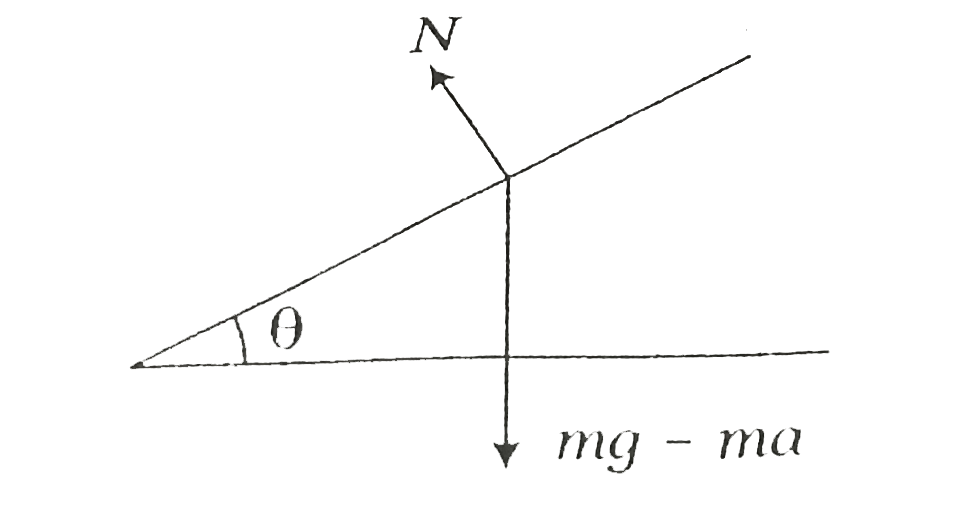 lt brgt ⇒ μ=tanθ=tan30∘=1√3
lt brgt ⇒ μ=tanθ=tan30∘=1√3
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Assertion and reason
28 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A block of mass is kept on an inclined plane of a lift moving down with acceleration of 2ms−2 What should be the minimum coefficient of friction to let the block move down with constant velocity?

View SolutionFriction coefficient between block and inclined plane is [μ=1√3] if lift is moving vertically down with constant acceleration a then the value of acceleration a so that block moves down with constant velocity is
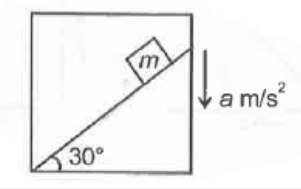
View Solution
Knowledge Check
A block of mass is kept on an inclined plane of a lift moving down with acceleration of 2ms−2 What should be the minimum coefficient of friction to let the block move down with constant velocity?
 Aμ=1√3Bμ=0.4Cμ=0.8Dμ= not defined
Aμ=1√3Bμ=0.4Cμ=0.8Dμ= not definedA block of mass m is kept on an inclined plane of a lift moving down with acceleration of 2m/s2 . What should be the coefficient of friction for the block to move down with constant velocity relative relative to lift?
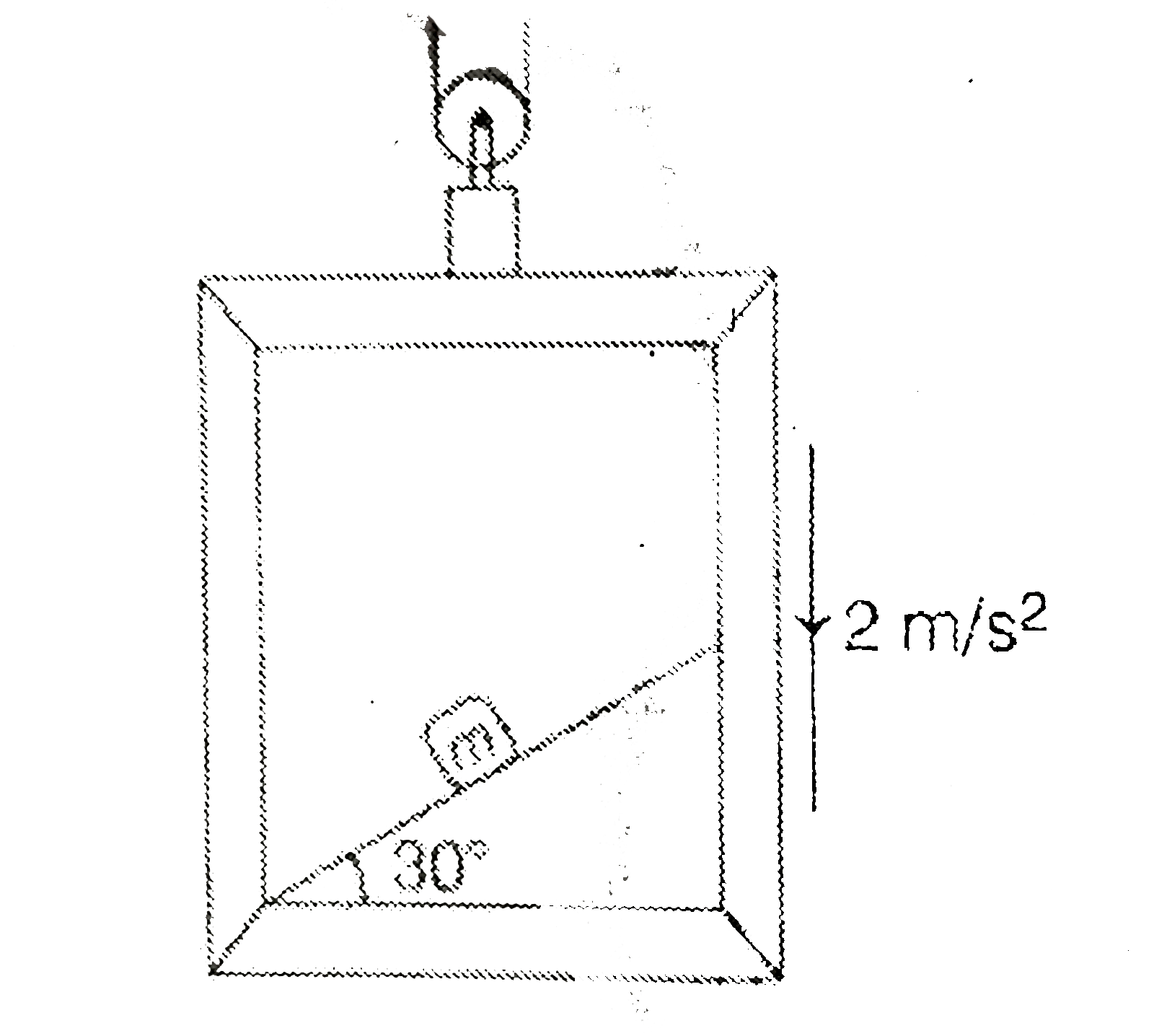 Aμ=1√3Bμ=0.4Cμ=0.8Dμ=0.5
Aμ=1√3Bμ=0.4Cμ=0.8Dμ=0.5A block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
AmgBmgsinθ√1+μ2CmgsinθD√(mgsinθ)2+(μmgcosθ)2
A block of mass 1kg is kept on the tilted floor of a lift moving down with acceleration 3ms−2. If the block is released from rest as shown, what will be the time taken by block to reach the bottom? What is the normal reaction on the block during the motion?

View SolutionA block of mass 'm' is placed on the floor of a lift, moving upward with an uniform acceleration a = g. (μis the coefficient of friction between block and the floor of lift). If a horizontal force of umg acts on the block, then horizontal acceleration of the body is .......
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View SolutionA block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
View Solution
