A body of weight 27N hangs on a long spring of such stiffness that an extra force of 9N stretches the spring by 0.05m. If the body is pulled downward and released, what is the period ?
To solve the problem step by step, we will follow these key points:
Step 1: Determine the Spring Constant (k)
Given that an extra force of F=9N stretches the spring by x=0.05m, we can use Hooke's Law, which states:
F=kx
Rearranging this gives us:
k=Fx
Substituting the values:
k=9N0.05m=180N/m
Step 2: Calculate the Mass (m)
The weight of the body is given as W=27N. We can relate weight to mass using the equation:
W=mg
Where g (acceleration due to gravity) is approximately 10m/s2. Rearranging for mass gives:
m=Wg
Substituting the values:
m=27N10m/s2=2.7kg
Step 3: Calculate the Period (T)
The formula for the period of a mass-spring system in simple harmonic motion is given by:
T=2π√mk
Substituting the values of m and k:
T=2π√2.7kg180N/m
Calculating the fraction:
2.7180=0.015
Now, taking the square root:
√0.015≈0.1225
Now, multiplying by 2π:
T≈2π×0.1225≈0.769s
Rounding gives us:
T≈0.78s
Final Answer
The period of the body is approximately 0.78s.
---
Given that an extra force of F=9N stretches the spring by x=0.05m, we can use Hooke's Law, which states:
The weight of the body is given as W=27N. We can relate weight to mass using the equation:
The formula for the period of a mass-spring system in simple harmonic motion is given by:
The period of the body is approximately 0.78s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A sand bag of mass m is hanging from a light spring of stiffness k. Find the elongation of the spring. If we pull the sand bag down by an additional distance x and release it, find its acceleration and maximum velocity of block.

View SolutionA block with a mass of 3.00kg is suspended from an ideal spring having negligible mass and stretches the spring by 0.2m.
(a) What is the force constant of the spring?
(b) What is the period of oscillation of the block if it is pulled down and released ?
View SolutionA block with a mass of 3.00kg is suspended from an ideal spring having negligible mass and stretches the spring by 0.2m.
(a) What is the force constant of the spring?
(b) What is the period of oscillation of the block if it is pulled down and released ?
View SolutionA block of massm=20g is attached to one end of an inextensible thread passing over two frictionless and massless pulleys as shown in figure. The spring constant of the spring is 2Nm. Suppose the blockis pulled downward and released .
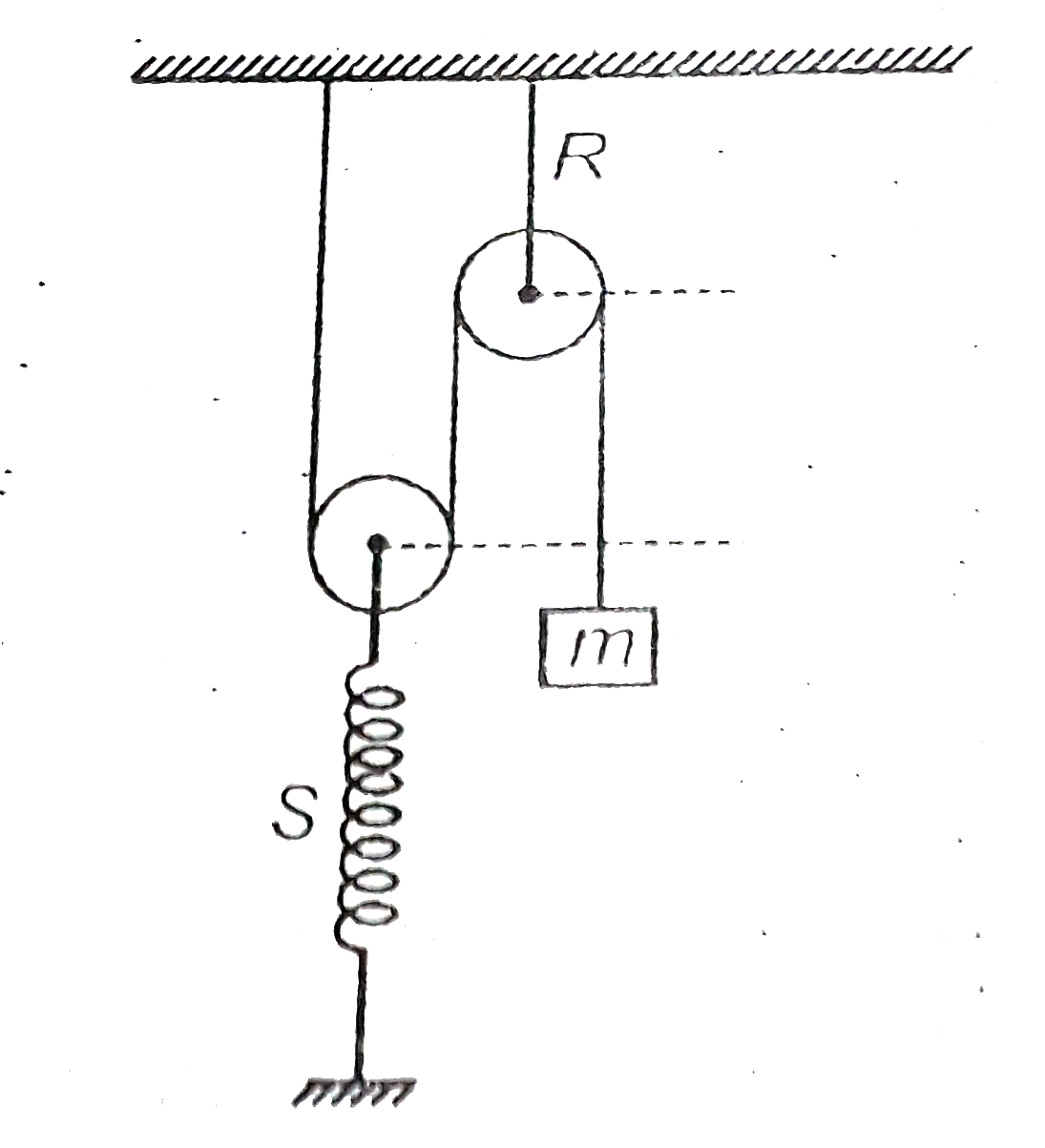
The natural frequency of oscialltion of system is Hz
View SolutionA body of mass 100 g is attached to a hanging spring force constant is 10N/m. The body is lifted until the spring is in its unstretched state and then released. Calculate the speed of the body when it strikes the table 15cm below the release point .
View SolutionA body of mass m is suspended from vertical spring and is set into simple harmonic oscillations of time period T. Next the spring is fixed at one end on a smooth horizontal table and same body is attached at the other end. The body is pulled slightly and then released to produce horizontal oscillations of the spring. The time period of horizontal oscillations is
View SolutionA spring has a natural length of 50 cm and a force constant of 2.0×103 Nm−1. A body of mass 10 kg is suspended from it and the spring is stretched. If the body is pulled down to a length of 58 cm and released, it executes simple harmonic motion. The net force on the body when it is at its lowermost position of its oscillation is (10x) newton. Find value of x. (Take g=10m/s2)
View SolutionA spring has a natural length of 50 cm and a force constant of 2.0×103 Nm−1. A body of mass 10 kg is suspended from it and the spring is stretched. If the body is pulled down to a length of 58 cm and released, it executes simple harmonic motion. The net force on the body when it is at its lowermost position of its oscillation is (10x) newton. Find value of x. (Take g=10m/s2)
View SolutionA block of mass 100g attached to a spring of stiffness 100N/m is lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collision with the wall is elastic then find the time period of oscillations.

View SolutionOne end of a fixed spring is pulled by an average force of 10N through a distance of 5cm, find the work done by the spring.
View Solution
