A sand bag of mass m is hanging from a light spring of stiffness k. Find the elongation of the spring. If we pull the sand bag down by an additional distance x and release it, find its acceleration and maximum velocity of block.

Since F=−kxˆj and downward force =+mgˆj
ΣFy=0
mg=kΔx
Δx=mgK
If we apply addition force to pull it down by distance x, then FBD
Upward forces are =k(x+Δx)
Downward force =F+mg
If we remove from F then ΣFy=may
K(x+Δx)−mg=ma
Maximum acceleration,
a=k(Δx+x)m−g
a=kΔxm+kxm−g=kxm
Maximum velocity: F=kx
ma=kx⇒vdvdx=kxm⇒v22=kx22m
v=√kmx.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct
75 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.3
19 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionTwo identical particles each of mass m are connected by a light spring of stiffness K. The initial deformation of the spring when the system was at rest, x0. After releasing the system, if one of the particles has a speed v and the deformation of the spring is x, find the speed of the other particle neglecting friction.
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA mass M is suspended from a light spring. An additional mass m added to it displaces the spring further by distance x then its time period is
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo identicle particles A and B, each of mass m, are interconnected by a spring of stiffness k. If particle B experiences a forec F and the elongation of the spring is x, the acceleration of particle B relative to particle A is equal to

View SolutionA block of mass m fitted with a light spring of stiffness k and natural length l0 kept on a smooth radial groove made on a disc rotaing with a constant angular axis . If the block is released slowly . Find the maximum elongation of the spring

View SolutionTwo blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View SolutionA smooth block of mass m is connected with a spring of stiffness k(=20Nm−1 )and natural length l0=0.25m. If the block is pulled such that the new length of the spring becomes l=0.3m, find the acceleration of the block at the moment when it is released from given positon.
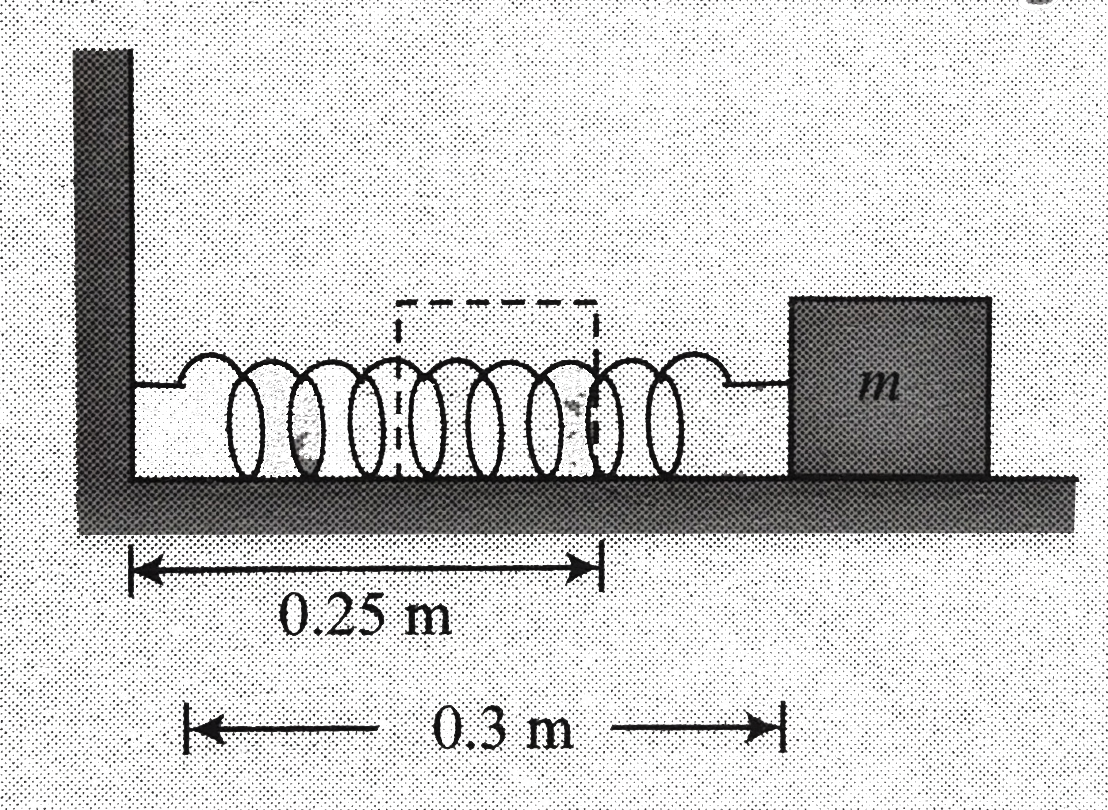
View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.

a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View Solution
