A bolt is passed through a pipe and a nut is just tightened. Coefficients of linear expansion for bolt and pipe material are αb and αp respectively. If the assembly is heated then:
A tensile stress will be induced in the bolt if αb<αp
A compresive stress will be induced in the bolt if αb<αp
A compressive stress will be induced in the bolt is αb=αp
No stress will be iduced in the bolt if αb>αp
To solve the problem, we need to analyze the behavior of the bolt and the pipe when the assembly is heated, considering the coefficients of linear expansion for both materials.
1. Understanding Linear Expansion:
- When a material is heated, it expands. The amount of expansion (ΔL) is directly proportional to the original length (L) and the temperature change (ΔT), given by the formula:
ΔL=α⋅L⋅ΔT
- Here, α is the coefficient of linear expansion for the material.
2. Define Variables:
- Let αb be the coefficient of linear expansion for the bolt.
- Let αp be the coefficient of linear expansion for the pipe.
- Let Lb be the original length of the bolt.
- Let Lp be the original length of the pipe.
3. Expansion of Bolt and Pipe:
- When the assembly is heated:
- The change in length of the bolt:
ΔLb=αb⋅Lb⋅ΔT
- The change in length of the pipe:
ΔLp=αp⋅Lp⋅ΔT
4. Comparing Expansions:
- We will analyze three cases based on the relationship between αb and αp.
5. Case 1: αb<αp:
- The bolt expands less than the pipe. Therefore:
ΔLb<ΔLp
- As the pipe tries to expand more than the bolt, it will exert a compressive force on the bolt, inducing tensile stress in the bolt.
6. Case 2: αb=αp:
- Both the bolt and the pipe expand equally:
ΔLb=ΔLp
- There is no relative movement between the bolt and the pipe, resulting in no stress being induced in either.
7. Case 3: αb>αp:
- The bolt expands more than the pipe:
ΔLb>ΔLp
- In this case, the bolt will not be constrained by the pipe, leading to no stress being induced in the bolt.
Conclusion:
- If αb<αp: Tensile stress is induced in the bolt.
- If αb=αp: No stress is induced in the bolt.
- If αb>αp: No stress is induced in the bolt.
- When a material is heated, it expands. The amount of expansion (ΔL) is directly proportional to the original length (L) and the temperature change (ΔT), given by the formula:
ΔL=α⋅L⋅ΔT
- Here, α is the coefficient of linear expansion for the material.
- Let αb be the coefficient of linear expansion for the bolt.
- Let αp be the coefficient of linear expansion for the pipe.
- Let Lb be the original length of the bolt.
- Let Lp be the original length of the pipe.
- When the assembly is heated:
- The change in length of the bolt:
ΔLb=αb⋅Lb⋅ΔT
- The change in length of the pipe:
ΔLp=αp⋅Lp⋅ΔT
- We will analyze three cases based on the relationship between αb and αp.
- The bolt expands less than the pipe. Therefore:
ΔLb<ΔLp
- As the pipe tries to expand more than the bolt, it will exert a compressive force on the bolt, inducing tensile stress in the bolt.
- Both the bolt and the pipe expand equally:
ΔLb=ΔLp
- There is no relative movement between the bolt and the pipe, resulting in no stress being induced in either.
- The bolt expands more than the pipe:
ΔLb>ΔLp
- In this case, the bolt will not be constrained by the pipe, leading to no stress being induced in the bolt.
- If αb<αp: Tensile stress is induced in the bolt.
- If αb=αp: No stress is induced in the bolt.
- If αb>αp: No stress is induced in the bolt.
Topper's Solved these Questions
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - NUMERICAL MCQs SINGLE OPTIONS CORRECT
81 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems
107 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
66 Videos
Similar Questions
A composite bar of length L=L1+L2 is made from a bar of material 1 and length L1 attached to a bar of material 2 and length L2. Find the effective linear expansion α of this bar.The coefficinets of linear expansion of the material of the rods are α1 and α2 respectively.
View SolutionTwo rods of material X sandwich another rod of material Y as shown in figure. At temperature t, the three rods are in a state of zero strailn and of length L and riveted to each other in this state. If the temperature of the system increases to T+ΔT, find the final length of the system of the three rods. Given that the coefficients of linear expansions of the roods and their Young's modulus for material X and Y are alpnax,αy,Yx and Yy respectively. Consider αy>αx.

View Solution
Knowledge Check
Two rods of lengths L1 and L2 are welded together to make a composite rod of length (L1+L2). If the coefficient of linear expansion of the materials of the rod are α1 and α2 respectively. The effective coefficient of linear expansion of the composite rod is
AL1α1−L2α2L1+L2BL1α1+L2α2L1+L2C√α1α2Dα1+α22A metallic pipe with nut and bolt assembly is shown in the figure. as is the coefficient of linear expansion for bolt and ∝p( when ∝B>∝p) is for the material of pipe. The arrangement is heated then
(##TRG_PHY_MCQ_XII_C09_E04_001_Q01.png" width="80%">Atensile stress is developed in the boltBcompressive stress is developed in the bolt.Cno stress is developed in the boltDBoth (A) and (B)A bimetallic strip is formed out of two identical strips one of copper and the other of brass. The co-efficients of linear expansion of the two metals are αC and αB. On heating, the the strip bends to form an are of radius of curvature R. Then R is
Aproportional to ΔTBinversely proportional to ΔTCproportional to |αB−αC|DInversely proportional to |αB−αC|
Two straight metallic strips each of thickness t and length l are rivetted together. Their coefficients of linear expansions areα1andα2. If they are heated through temperature ΔT, the bimetallic strip will bend to form an arc of radius
View SolutionThe length of two metallic rods at temperatures θ are LA and LB and their linear coefficient of expansion are αA and αB respectively. If the difference in their lengths is to remain constant at any temperature then
View SolutionTwo rods of length l1 and l2 are made of material whose coefficient of linear expansion are α1 and α2 , respectively. The difference between their lengths will be independent of temperatiure if l1/l2 is to
View SolutionIf αc and αf denote the numerical values of coefficient of linear expansion of a solid, expressed per .0C and per .0F respectively, then
View SolutionTwo rods of different materials are placed between massive walls as shown in figure. The cross section of the rods is A, their moduil of elastricity are E1 and E2 respectively. If rods are heated by t degrees, then (coefficients of liner expansion of material of rods are α1 and α2 respectively)
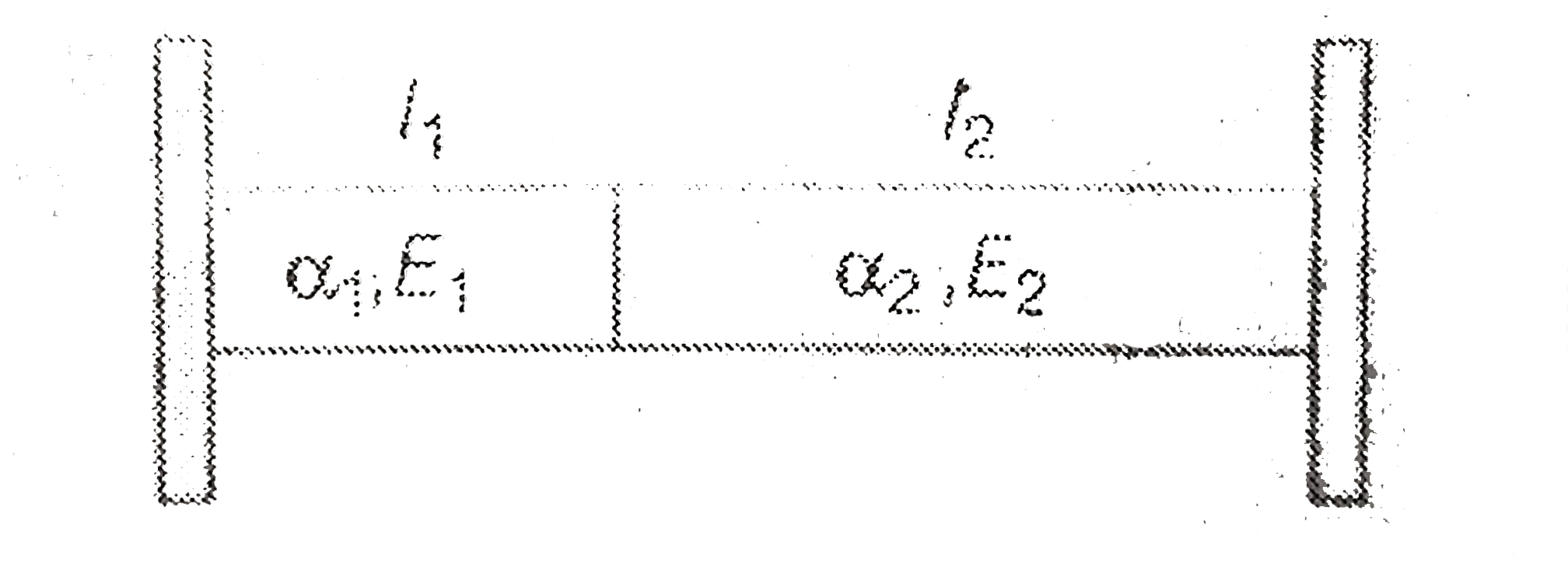
View Solution
