A box B of mass M hangs from an ideal spring of force constant k. A small particle, also of mass M, is stuck to the ceiling of the box and the system is in equilibrium. The particle gets detached from the ceiling and falls to strike the floor of the box. It takes time t for the particle to hit the floor after it gets detached from the ceiling. The particle, on hitting the floor, sticks to it and the system thereafter oscillates with a time period T. Find the height H of the box if it is given that t=T6√2. Assume that the floor and ceiling of the box always remian horizontal.

The correct Answer is:H=Mg2k(1+π29)
Step by step video, text & image solution for A box B of mass M hangs from an ideal spring of force constant k. A small particle, also of mass M, is stuck to the ceiling of the box and the system is in equilibrium. The particle gets detached from the ceiling and falls to strike the floor of the box. It takes time t for the particle to hit the floor after it gets detached from the ceiling. The particle, on hitting the floor, sticks to it and the system thereafter oscillates with a time period T. Find the height H of the box if it is given that t=(T)/(6sqrt(2)). Assume that the floor and ceiling of the box always remian horizontal. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- ROTATIONAL MOTIONBOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS
159 Videos
- SURFACE TENSIONBOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension
33 Videos
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
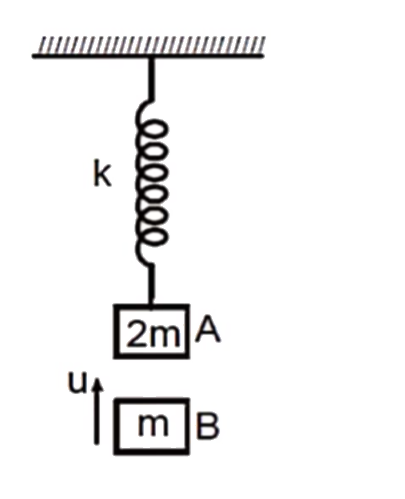
View Solution
Knowledge Check
A cage of mass M hangs from a light spring of force constant k. A body of mass m falls from height h inside the cage and stricks to its floor. The amplitude of oscillations of the cage will be-
_E01_061_Q01.png) A(2mghk)1/2B(k2mgh)1/2CmgkD(mgk)1/2
A(2mghk)1/2B(k2mgh)1/2CmgkD(mgk)1/2A particle of mass m is hanging vertically by an ideal spring of force constant K . If the mass is made to oscillate vertically, its total energy is
AMaximum at extreme positionBMaximum at mean positionCMinimum at mean positionDSame at all positionA particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12
As shown in the figure a block of mass m is hung from the ceiling by the system of springs consisting of two layers. The force constant of each of the springs is k. The frequency of the vertical oscillations of the block is
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is

View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionA rope of length L and mass m hangs freely from the ceiling. The velocity of transverse wave as a function of position x from the bottom is proportional to
View Solution
