A box slides down an inclined plane (incline angle=40∘). The mass of the block, m, is 40 kg, the coefficient of kinetic friction between the box and the ramp, μk, is 0.3, and the length of the ramp, d, is 10m. (Use: sin40∘=0.6andcos40∘=0.8).

Q. how much work is done by gravity?
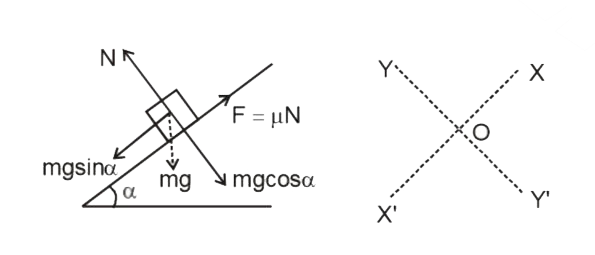
Remember that the force that's directly responsible for pulling the box down the plane (F∣∣) is the component of the gravitational force that's parallel to the ramp: Fwsinθ=mgsinθ (where θ is the incline angle). This component is parallel to the motion, so the work done by gravity is:
Wby gravity=(mgsinθ)=(40kg)(10N/kg)(sin40∘)(10m)=2,400J
Notice that the work done by gravity is positive as we would expect it to be, since gravity is helping the motion. also, be careful with the angle θ. the general definition of work reads W=(Fcosθ)d, where θ is the angle between F and d. however, the angle between Fwandd is not 40∘ here, so the work done by gravity is not (mgcos40∘)d. the angle θ used in the calculation above is the incline angle. this is why W=F∣∣d is a useful way of writing the formula.
Topper's Solved these Questions
Similar Questions
A 20kg box is gently placed on a rough inclined plane of inclination 30∘ with horizontal. The coefficient of sliding friction between the box and the plane is 0.5.Find the acceleration of the box down the incline.
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View Solution
Knowledge Check
A block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
AmgBmgsinθ√1+μ2CmgsinθD√(mgsinθ)2+(μmgcosθ)2A block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
Amgsinθ√1+μ2B√(mgsinθ)2+(μmgcosθ)2CmgsinθDmgA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1Dμmgθ
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA block of mass 1 kg slides down on a rough inclined plane of inclination 60∘ starting from its top. If the coefficient of kinetic friction is 0.5 and length of the plane is 1 m , then work done against friction is (Take g=9.8m/s2)
View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View SolutionA plank of mass 3m is placed on a rough inclined plane and a man of mass m walks down the board. If the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of does not slide is:

View Solution
