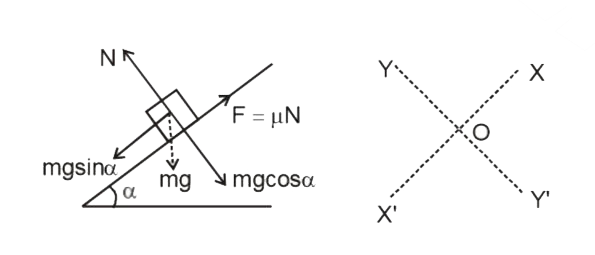
A box slides down an inclined plane (incline angle=40∘). The mass of the block, m, is 40 kg, the coefficient of kinetic friction between the box and the ramp, μk, is 0.3, and the length of the ramp, d, is 10m. (Use: sin40∘=0.6andcos40∘=0.8).

Q. How much work is done by friction?
The strength of the normal force is Fwcosθ (where θ is the incline angle), so the strength of the friction force is Ff=μkFN=μkFwcosθ=μkmgcosθ. Since Ff is antiparallel to d, the cosine of the angle between these vector (180∘) is -1, so the work done by friction is
Wby friction=−Fid=−(μkmgcosθ)(d)
=(−0.3)(40kg)(10N/kg)(cos40∘)(10m)
=−960J ltbr Notice that thw work done by friction is negative, as we expect it to be, since friction is opposing the motion.
Topper's Solved these Questions
Similar Questions
A block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionA 20kg box is gently placed on a rough inclined plane of inclination 30∘ with horizontal. The coefficient of sliding friction between the box and the plane is 0.5.Find the acceleration of the box down the incline.
View Solution
Knowledge Check
A block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
AmgBmgsinθ√1+μ2CmgsinθD√(mgsinθ)2+(μmgcosθ)2A block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
Amgsinθ√1+μ2B√(mgsinθ)2+(μmgcosθ)2CmgsinθDmgA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
A(a) 1.6B(b) 4.0C(c) 2.0D(d) 2.5
A block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionBlock of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
View Solution
