A boy on a train of height h1 projects a coin his friend of height h2 standing on the same train, with a velocity v relative to the train, at an angle θ with horizontal. If the train moves with a constant velocity v' in the direction of x - motion of the coin, find the
(a) distance between the boys so that the second boy can catch the coin,
(b) maximum height attained by the coin, and
( c) speed with which the second boy catches the coin relative to himself (train) and ground.
The correct Answer is:(a) h2−h1=xtanθ−gx22v2cos2θ from here, we will get two values of x, both can be valid ;
(b) H=h1+v2sin2θ2g ;
( c) √v2−2g(h2−h1).
(a) Taking point A as origin
y=xtanθ−gx22u2cos2θ
⇒h2−h1=xtanθ−gx22y2cos2θ
From here, we will get two values of x, both can be valid.
(b) Maximum height H=h1+v2sin2θ2g
( c) w.r.t. train :
vx=vcosθ
v2y=(vsinθ)2−2g(h2−h1)
Final speed :
vf=√v2x+v2y=√(vcosθ)2+(vsinθ)2−2g(h2−h1)
=√v2−2g(h2−h1)
w.r.t ground : vx=v'+vcosθ
v2y=(vsinθ)2−,2g(h2−h1)
Final speed : vf=√v2x+v2y.
 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Rain is falling vertically downwards with a speed of 4kmh−1. A girl moves on a straight road with a velocity of 3kmh−1. The apparent velocity of rain with respect to the girl is.
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA particle is moving with constant speed in a circle as shown in (Fig. 5.163). Find the angular velocity of the particle A with respect to fixed point BandC if angular velocity with respect to Oisω.
 .
.
View SolutionForm a lift moving upwards with a uniform acceleration a=2ms−2,manthrousaballverticallyupwardswithavelcoityv=12ms−1 relative to the lift. The ball comes back to the man after a time t. Find the value of t in seconds.
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
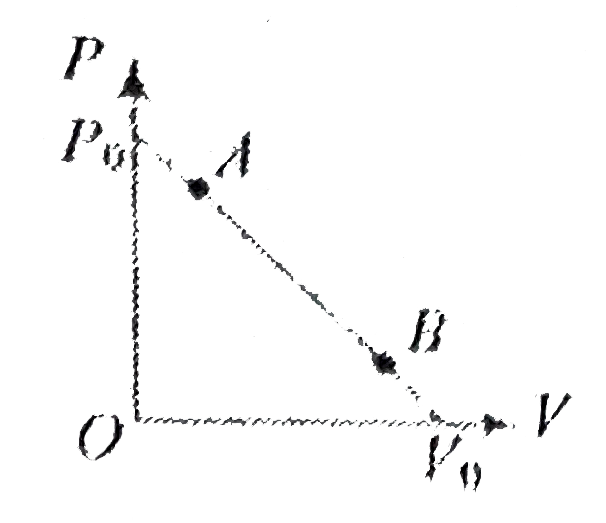
The absolute temperature T versus volume V for the given process is
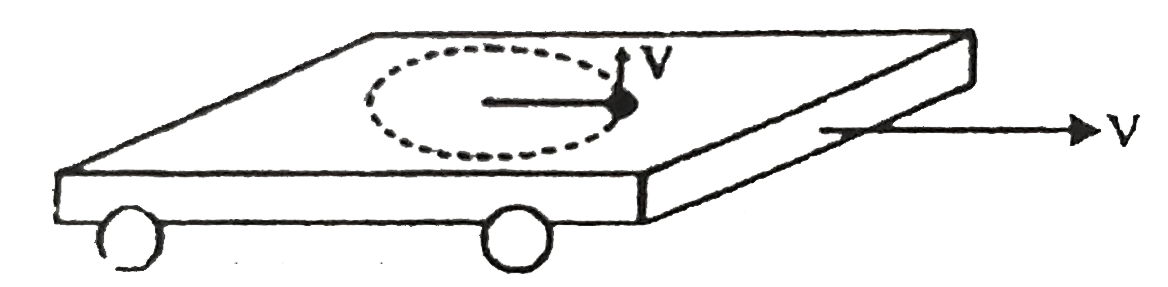
View SolutionOn a train moving along east with a constant speed v, a boy revolves a bob with string of length l on smooth surface of a train, with equal constant speed v relative to train. Mark the correct option(s).
View SolutionA boy sitting at the rear end of a railway compartment of a train, running at a constant acceleration on horizontal rails throws towards the fore end of the compartment with a muzzle velocity of 20m/sec at an angle 37∘ above the horizontal, when the train is running at a speed of 10 m/sec. If the same boy catches the ball without moving from his seat and at the same height of projection,find the speed of the train at the instant of his catching the ball.
View SolutionA train is moving forward with a horizontal acceleration a. A man sitting in the train drops a coin on the floor of the train . The acceleration of the coin w.r.t man is
View Solutionएक ट्रैन समान त्वरण a से एक सीधी रेखा पर चल रही है। ट्रैन में खड़ा एक लड़का 10 मी/से के वेग से क्षैतिज 60∘ के कोण पर एक एक गेंद आगे की ओर फेंकता है। लड़का ट्रैन में 1.15 भी आगे चलकर गेंद को उसकी प्रारम्भिक ऊंचाई पर पकड़ता है । ट्रैन के त्वरण का मान मी/से2 मैं है।
View SolutionA train is moving along a straight line with a constant acceleration 'a' . A boy standing in the train throws a ball forward with a speed of 10m/s, at an angle of 60(∘) to the horizontal. The boy has to move forward by 1.15m inside the train to catch the ball back at the initial height . the acceleration of the train , in m/s2 , is
View SolutionIn a moving train, a boy faces the engine and throws the coin upwards in the corner, which falls on the boy's back. Then the train-
View SolutionIf a boy on a moving train faces the engine and throws the coin upright in the corner, it falls behind the boy, then the train - (A) Moving forward with speed (B) Running backwards (C) Going forward with slowdown (D) Moving forward with acceleration
View Solutionएक ट्रेन समान त्वरण 'a' से एक सीधी रेखा पर चल रही है। ट्रेन में खड़ा एक लड़का 10 m/s के वेग से क्षैतिज से 60∘ के कोण पर एक गेंद आगे की ओर फेंकता है। लड़का ट्रेन में 1.15 m आगे चलकर गेंद को उसकी प्रारम्भिक ऊँचाई पर पकड़ता है। ट्रेन के त्वरण का मान m/s2 में है।
View SolutionA train is running on a straight line with the same acceleration 'a'. A boy standing in a train with a velocity of 10 m / s horizontally 60^(@) Throws a ball forward at an angle of. Boy on train 1.15 m moves forward and catches the ball at its initial height. Train acceleration value m//s^(2) Is in
View SolutionA boy on a train of height h1 projects a coin his friend of height h2 standing on the same train, with a velocity v relative to the train, at an angle θ with horizontal. If the train moves with a constant velocity v' in the direction of x - motion of the coin, find the
(a) distance between the boys so that the second boy can catch the coin,
(b) maximum height attained by the coin, and
( c) speed with which the second boy catches the coin relative to himself (train) and ground.
View Solution
