A bulb B a capacitor C are connected in series to an a.c. source. A dielectric slab is now introduced between the plates of the capacitor. How will the brightness of bulb change ?
To solve the problem of how the brightness of the bulb changes when a dielectric slab is introduced between the plates of a capacitor connected in series with an AC source, we can follow these steps:
Step 1: Understand the Circuit Configuration
We have a bulb (B) and a capacitor (C) connected in series to an AC source. The brightness of the bulb depends on the current flowing through the circuit.
Hint: Remember that the brightness of a bulb is directly proportional to the current flowing through it.
Step 2: Analyze the Effect of the Dielectric
When a dielectric slab is introduced between the plates of the capacitor, the capacitance (C) of the capacitor increases. The new capacitance can be represented as C′=kC, where k is the dielectric constant (greater than 1).
Hint: Increasing capacitance affects the capacitive reactance of the circuit.
Step 3: Calculate the Capacitive Reactance
The capacitive reactance (XC) is given by the formula:
XC=1ωC
where ω=2πf (angular frequency) and f is the frequency of the AC source.
With the introduction of the dielectric, the new capacitive reactance becomes:
X′C=1ωC′
Since C′=kC, we have:
X′C=1ωkC
This shows that X′C<XC because k>1.
Hint: Remember that a lower capacitive reactance means less opposition to the current flow.
Step 4: Determine the Impedance of the Circuit
The total impedance (Z) of the circuit is given by:
Z=√R2+X2C
Initially, the impedance is:
Z=√R2+X2C
After introducing the dielectric, the new impedance becomes:
Z′=√R2+X′2C
Since X′C<XC, it follows that Z′<Z.
Hint: Lower impedance results in higher current in the circuit.
Step 5: Calculate the Current in the Circuit
The current (I) in the circuit can be calculated using Ohm's law for AC circuits:
I=EZ
where E is the voltage of the AC source.
With the new impedance:
I′=EZ′
Since Z′<Z, it follows that I′>I.
Hint: An increase in current leads to an increase in brightness.
Step 6: Conclusion
Since the current in the circuit increases when the dielectric slab is introduced, the brightness of the bulb will also increase.
Final Answer: The brightness of the bulb increases.
We have a bulb (B) and a capacitor (C) connected in series to an AC source. The brightness of the bulb depends on the current flowing through the circuit.
When a dielectric slab is introduced between the plates of the capacitor, the capacitance (C) of the capacitor increases. The new capacitance can be represented as C′=kC, where k is the dielectric constant (greater than 1).
The capacitive reactance (XC) is given by the formula:
XC=1ωC
where ω=2πf (angular frequency) and f is the frequency of the AC source.
X′C=1ωC′
Since C′=kC, we have:
X′C=1ωkC
This shows that X′C<XC because k>1.
The total impedance (Z) of the circuit is given by:
Z=√R2+X2C
Initially, the impedance is:
Z=√R2+X2C
After introducing the dielectric, the new impedance becomes:
Z′=√R2+X′2C
Since X′C<XC, it follows that Z′<Z.
The current (I) in the circuit can be calculated using Ohm's law for AC circuits:
I=EZ
where E is the voltage of the AC source.
I′=EZ′
Since Z′<Z, it follows that I′>I.
Since the current in the circuit increases when the dielectric slab is introduced, the brightness of the bulb will also increase.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
Two identical capacitors are connected as shown in fignre. A dielectric slab is introduced between the plates of one of the capacitors so as to fill the gap, the battery remaining connected. What will be the capacitance, the charge, potential difference and stored energy for each capacitor?
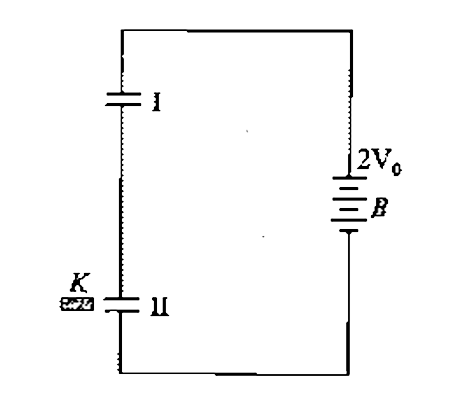 View Solution
View SolutionTwo identical capacitors are connected as shown. A dielectric slab Is introduced between the plates of one of the capacitors so as to fill the gap, the battery remaining connected. Compare the capacitance, the charge, potential difference and stored energy of each capacitor before and arter introducting of dielectric slab.
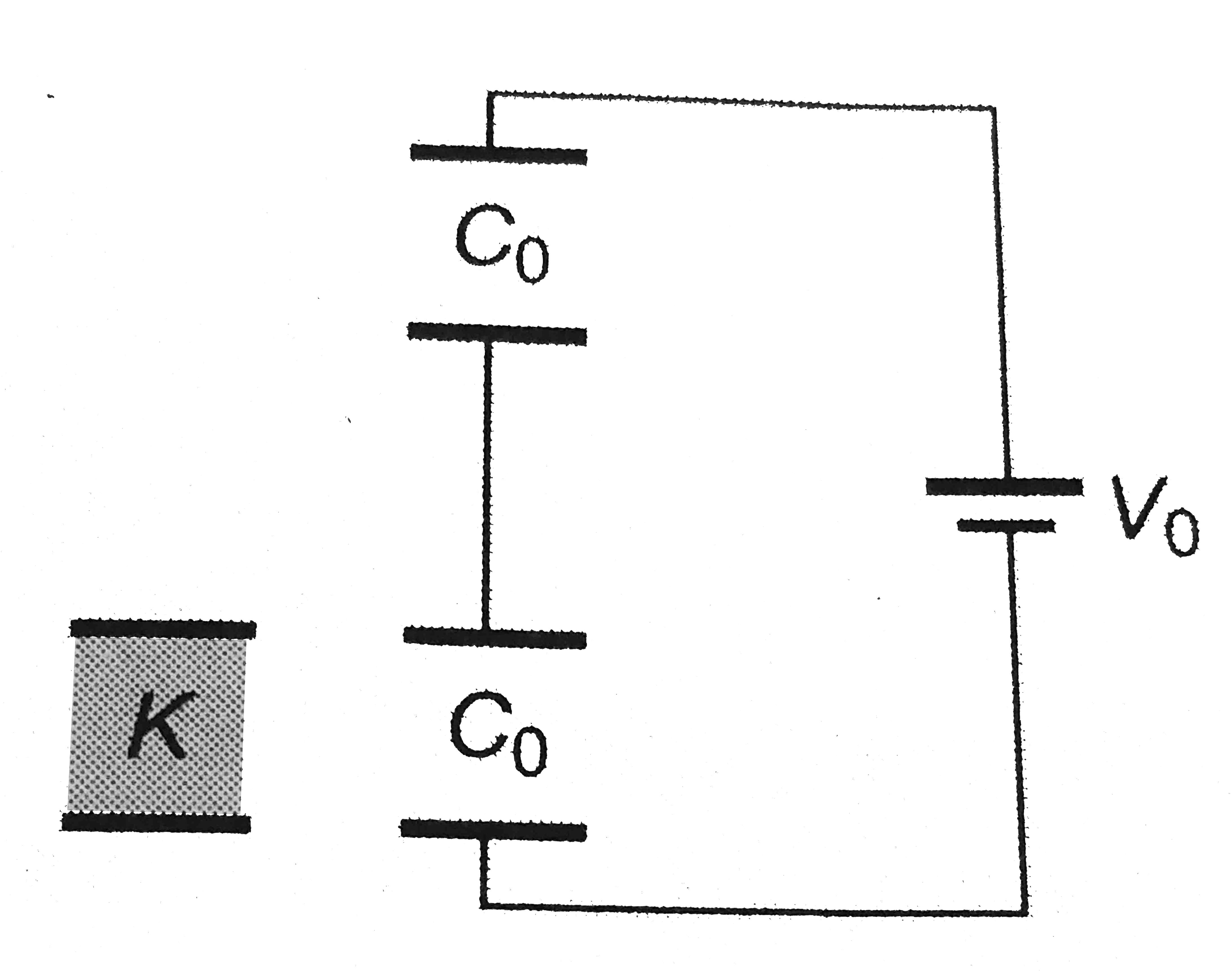 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A capacitor and a bulb are connected in series with a source of alternating emf. If a dielectric slab is inserted between the plates of the capacitor, then
AThe brightness of the bulb decreasesBThe brightness of the bulb increasesCThe brightness of the bulb remains sameDThe brightness of the bulb becomes zero - Question 2 - Select One
A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreases - Question 3 - Select One
Two identical parallel plate capacitors are connected in series to a battery of 100V. A dielectric slab of dielectric constant 4.0 is inserted between the plates of second capacitor. The potential difference across the capacitors will now be respectively
A50V,50VB80V,20VC20V,80VD75V,25V
Explain why the capacitance of a parallel plate capacitor increases when a dielectric slab is introduced between the plates.
View SolutionA bulb and a capacitor are connected in series to an a.c. source of variable frequency. How will the brightness of the bulb change on increasing the frequency of the a.c. source. Give reason.
View SolutionThere is an air capacitor with capacitance C, charged to a potential difference of V. If the capacitor is isolated from the battery after charging, and then a dielectric slab is inserted in between the plates of capacitor. How will the energy stored in this capacitor change?
View SolutionA capacitor of capacitance C is connected to a battery of V volts.A dielectric k=73 is introduced betwene the plates of the capacitor when battery is connected.The ratio of energies stored in the capacitor without dielectric and with dielectric..
View SolutionWhile a capacitor remains connected to a battery and dielectric slab is applied between the plates, then
View Solution

