A bullet fired at an angle of 30∘ with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 away? Assume the muzzle speed to be fixed and neglect air resistance.
To determine if a bullet fired at a fixed muzzle speed can hit a target 5.0 km away after already hitting a target 3.0 km away at an angle of 30 degrees, we can follow these steps:
Step 1: Understand the Range Formula
The range R of a projectile launched at an angle θ with an initial speed u is given by the formula:
R=u2sin(2θ)g
where g is the acceleration due to gravity (approximately 9.81m/s2).
Step 2: Calculate u2g for the First Case
Given that the bullet hits the ground 3.0 km away when fired at an angle of 30 degrees, we can set up the equation:
3000=u2sin(60∘)g
where sin(60∘)=√32.
Rearranging gives:
u2g=3000⋅2√3=6000√3≈3464.1m
Step 3: Determine Maximum Range
The maximum range Rmax occurs at an angle of 45 degrees:
Rmax=u2g
From our previous calculation, we have:
Rmax≈3464.1m
Step 4: Compare Maximum Range with Target Distance
The maximum range calculated is approximately 3464.1 m, which is less than the desired target distance of 5000 m (5 km). Therefore, it is impossible to hit a target 5 km away with the given muzzle speed.
Conclusion
Since the maximum range achievable with the fixed muzzle speed is less than 5 km, it is not possible to hit a target at that distance by adjusting the angle of projection.
---
The range R of a projectile launched at an angle θ with an initial speed u is given by the formula:
R=u2sin(2θ)g
where g is the acceleration due to gravity (approximately 9.81m/s2).
Given that the bullet hits the ground 3.0 km away when fired at an angle of 30 degrees, we can set up the equation:
3000=u2sin(60∘)g
where sin(60∘)=√32.
u2g=3000⋅2√3=6000√3≈3464.1m
The maximum range Rmax occurs at an angle of 45 degrees:
Rmax=u2g
From our previous calculation, we have:
Rmax≈3464.1m
The maximum range calculated is approximately 3464.1 m, which is less than the desired target distance of 5000 m (5 km). Therefore, it is impossible to hit a target 5 km away with the given muzzle speed.
Since the maximum range achievable with the fixed muzzle speed is less than 5 km, it is not possible to hit a target at that distance by adjusting the angle of projection.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.3
6 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Assertion And Reason
10 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.1
5 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A bullet fired at an angle of 30∘ with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to be fixed and neglect air resistance.
View SolutionA bullet is fired at an angle of 15∘ with the horizontal and it hits the ground 3 km away. Can we hit a target at a distance of 7 km by just adjusting its angle of projection ?
View SolutionA bullet fired at an angle of 60∘ with the vertical hits the levelled ground at a distance of 200 m . Find the distance at which the bullet will hit the ground when fired at angle of 30∘. (with same speed).
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.

Find the elevation angle ∠θ=∠OAC:
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
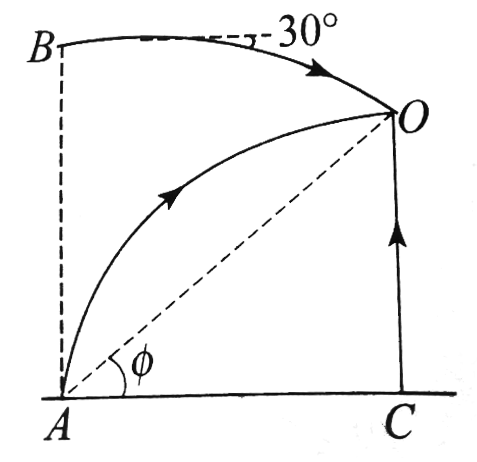
Find the time in which bullets will collide (seconds ):
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
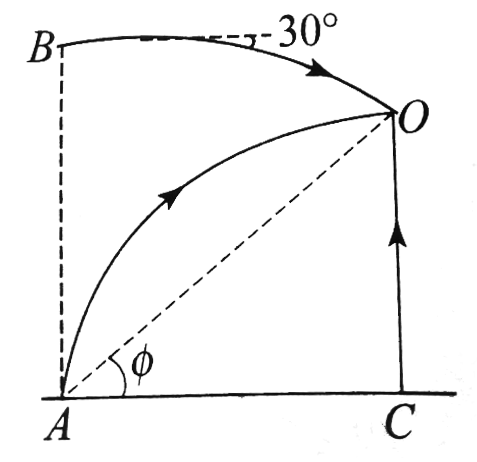
Find the velocity of bullet at A:
View SolutionA ball is projected at an angle of 30∘ above with the horizontal from the top of a tower and strikes the ground in 5s at an angle of 45∘ with the horizontal. Find the height of the tower and the speed with which it was projected.
View SolutionA particle aimed at a target projected with an angle 15∘ with the horizontal is short of the target by 10m .If projected with an angle of 45∘ is away from the target by 15m then the angle of projection to hit the target is
View SolutionA ball is projected from a point on the floor wilth a speed of 15 m/s at an angle of 600 with the horizontal. Will ilt hit a vertical wall 5 m away from the point of projection and perpendiculaer to the plane of projection without and perpendicular to the plane of projection without hitting the floor? will the answer differ if the wall is 22 m away?
View SolutionA particle projected from ground moves at angle 45∘ with horizontal one second after projection and speed is minimum two seconds after the projection The angle of projection of particle is [ Neglect the effect of air resistance )
View Solution
