A bullet fired at an angle of 60∘ with the vertical hits the levelled ground at a distance of 200 m . Find the distance at which the bullet will hit the ground when fired at angle of 30∘. (with same speed).
The correct Answer is:200 m.
To solve the problem, we need to find the horizontal range of a bullet fired at an angle of 30∘ with the same initial speed as when it was fired at 60∘. We know that the horizontal range R of a projectile is given by the formula:
R=u2sin2θg
where:
- u is the initial speed,
- θ is the angle of projection,
- g is the acceleration due to gravity.
Step 1: Identify the given values
From the problem, we know:
- The range R when the bullet is fired at 60∘ is 200m.
- The angle of projection for the first case, θ=60∘.
- The angle of projection for the second case, θ′=30∘.
Step 2: Write the range formula for both angles
For the angle 60∘:
R=u2sin(2×60∘)g
R=u2sin(120∘)g
For the angle 30∘:
R′=u2sin(2×30∘)g
R′=u2sin(60∘)g
Step 3: Set up the ratio of the ranges
Since the speed u and g are the same in both cases, we can set up the ratio of the ranges:
R′R=sin(60∘)sin(120∘)
Step 4: Substitute the known values
We know that:
- R=200m
- sin(60∘)=√32
- sin(120∘)=sin(180∘−60∘)=sin(60∘)=√32
Thus, substituting these values into the ratio:
R′200=√32√32=1
Step 5: Solve for R′
From the ratio, we find:
R′=200m
Conclusion
The distance at which the bullet will hit the ground when fired at an angle of 30∘ is also 200m.
- u is the initial speed,
- θ is the angle of projection,
- g is the acceleration due to gravity.
From the problem, we know:
- The range R when the bullet is fired at 60∘ is 200m.
- The angle of projection for the first case, θ=60∘.
- The angle of projection for the second case, θ′=30∘.
For the angle 60∘:
R=u2sin(2×60∘)g
R=u2sin(120∘)g
R′=u2sin(2×30∘)g
R′=u2sin(60∘)g
Since the speed u and g are the same in both cases, we can set up the ratio of the ranges:
R′R=sin(60∘)sin(120∘)
We know that:
- R=200m
- sin(60∘)=√32
- sin(120∘)=sin(180∘−60∘)=sin(60∘)=√32
R′200=√32√32=1
From the ratio, we find:
R′=200m
The distance at which the bullet will hit the ground when fired at an angle of 30∘ is also 200m.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -A Objective (one option is correct)
50 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -B Objective (one option is correct)
29 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :
1 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
A bullet is fired at an angle of 15∘ with the horizontal and it hits the ground 3 km away. Can we hit a target at a distance of 7 km by just adjusting its angle of projection ?
View SolutionA bullet fired at an angle of 30∘ with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to be fixed and neglect air resistance.
View Solution
Knowledge Check
A body is thrown with a velocity of 9.8 m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A3 sB2sC1.5 sD1 s
A bullet fired at an angle of 30∘ with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 away? Assume the muzzle speed to be fixed and neglect air resistance.
View SolutionTwo bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit the ground first?
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
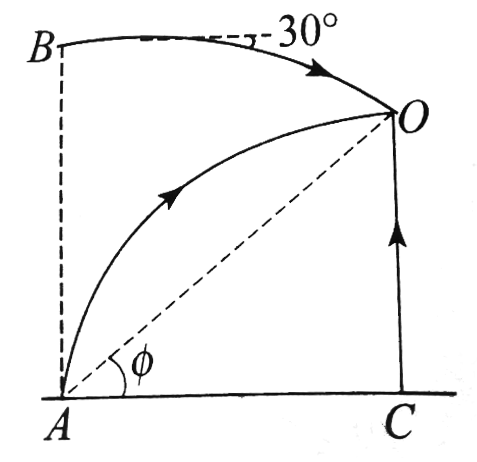
Find the time in which bullets will collide (seconds ):
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.

Find the elevation angle ∠θ=∠OAC:
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
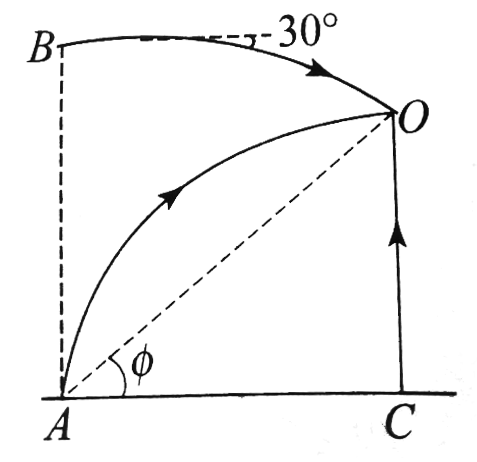
Find the velocity of bullet at A:
View SolutionA projectile projected with initial velocity 20m/s and at and angle of 30∘ from horizontal. Find the total work done when it will hit the ground.
View SolutionIn a region an electric field is setu!l with its strength E=15N/C and it makes an angle of 30° with the horizontal plane as shown in figure. A ball having a charge 2C, mass 3kg and coefficient of restitution with ground 0.5 is projected at an angle of 30° with the horizontal along the direction of electric field with speed 20 m/s. Find the horizontal distance travelled by ball from first hit with the ground to the second time when it hits the ground.

View Solution
