A bullet is fired from the bottom of the inclined plane at angle $θ = 37^{\circ}$ with the inclined plane. The angle of incline is $30^{\circ}$ with the horizontal. Find the
(a) position of the maximum height of the bullet from the inclined plane ,
(b) time of light ,
( c) range along the incline ,
(d) the value of $θ$ at which the range will be maximum ,
( e) maximum range.

Video Solution

Text Solution

Verified by Experts

(a) Taking axis system as shown in (Fig. S5.11)
At highest point, $v_{y} = 0$ . Therefore,
$v_{y}^{2} = u_{y}^{2} + 2 a_{y} y$
$\Rightarrow 0 = {(30)}^{2} - 2 g {cos 30}^{\circ} y$
$y = 30 \sqrt{3} m$ (maximum height)
(b) Again foe x coordiante,
$v_{y} = u_{y} + a_{y} t$
$0 = 30 - g {cos 30}^{\circ} \times t \Rightarrow t = 2 \sqrt{3} s$
Time of flight $T = 2 \times 2 \sqrt{3} s$
( c) Range, $x = u_{x} t + \frac{1}{2} a_{x} t^{2}$
= $40 \times 4 \sqrt{3} - \frac{1}{2} g {sin 30}^{\circ} \times ({\sqrt{3}}^{2})$
= $40 (4 \sqrt{3} - 3) m$
(d) $θ = \frac{π}{4} - \frac{30^{\circ}}{2} = 45^{\circ} - 15^{\circ} = 30^{\circ}$
( e) $\frac{u^{2}}{g (1 + sin β)} = \frac{50 \times 50}{10 (1 + \frac{1}{2})} = \frac{2500}{15} = \frac{500}{3} m$ .
.

A particle is projected from the inclined plane at angle $37^{\circ}$ with the inclined plane in upward direction with speed $10 m / s$ . The angle of inclined plane with horizontal is $53^{\circ}$ . Then the maximum height attained by the particle from the inclined plane will be-

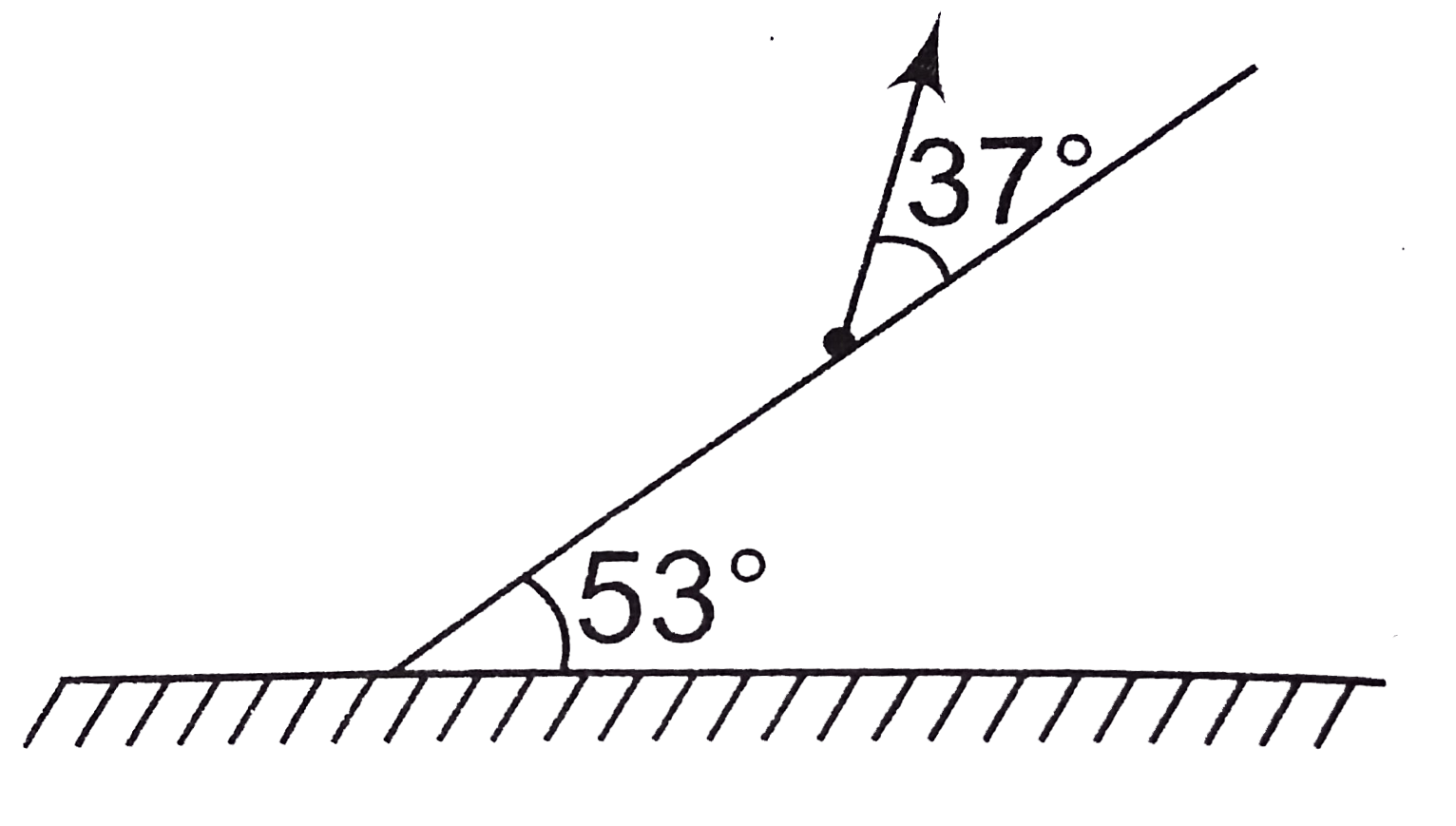A $3 m$
B $4 m$
C $5 m$
Dzero
A ball is projected from the bottom of an inclined plane of inclination $30^{\circ}$ , with a velocity of $30 m s^{- 1}$ , at an angle of $30^{\circ}$ with the inclined plane. If $g = 10 m s^{- 2}$ , then the range of the ball on given inclined plane is
A12 m
B60 m
C120 m
D600 m
A trolley containing a liquid slides down a smooth inclined plane of angle $α$ with the horizontal. Find the angle of inclination $θ$ of the free surface with the horizontal.

A $θ = \frac{α}{2}$
B $θ = 2 α$
C $θ = z e r o$
D $θ = α$