On an inclined plane of inclination 30∘, a ball is thrown at angle of 60∘ with the horizontal from the foot of the incline with a velocity of 10√3ms−1. Then the ball will hit the inclined plane in
1s
2s
2√3s
4√3s
The correct Answer is:b
To solve the problem of how long the ball will hit the inclined plane, we will follow these steps:
Step 1: Understand the Problem
We have a ball thrown from the foot of an inclined plane at an angle of 60∘ with the horizontal. The incline itself is at an angle of 30∘. The initial velocity of the ball is 10√3m/s. We need to find the time it takes for the ball to hit the inclined plane.
Step 2: Resolve the Initial Velocity
The initial velocity u can be resolved into two components:
- The horizontal component ux=ucos(60∘)
- The vertical component uy=usin(60∘)
Calculating these components:
- ux=10√3cos(60∘)=10√3⋅12=5√3m/s
- uy=10√3sin(60∘)=10√3⋅√32=15m/s
Step 3: Determine the Equations of Motion
The equations of motion for the ball can be described as:
- Horizontal motion: x=ux⋅t
- Vertical motion: y=uy⋅t−12gt2
Where g=10m/s2 is the acceleration due to gravity.
Step 4: Find the Equation of the Inclined Plane
The equation of the inclined plane can be derived from its angle:
- The slope of the incline is given by tan(30∘)=1√3.
- Thus, the equation of the inclined plane is y=1√3x.
Step 5: Substitute the Motion Equations into the Inclined Plane Equation
We substitute x and y from the motion equations into the inclined plane equation:
uy⋅t−12gt2=1√3(ux⋅t)
Substituting the values:
15t−12⋅10t2=1√3(5√3t)
This simplifies to:
15t−5t2=5t
Rearranging gives:
10t−5t2=0
Factoring out t:
t(10−5t)=0
This gives us two solutions:
1. t=0 (the time of projection)
2. 10−5t=0⇒t=2s
Step 6: Conclusion
The ball will hit the inclined plane after t=2s.
---
We have a ball thrown from the foot of an inclined plane at an angle of 60∘ with the horizontal. The incline itself is at an angle of 30∘. The initial velocity of the ball is 10√3m/s. We need to find the time it takes for the ball to hit the inclined plane.
The initial velocity u can be resolved into two components:
- The horizontal component ux=ucos(60∘)
- The vertical component uy=usin(60∘)
- ux=10√3cos(60∘)=10√3⋅12=5√3m/s
- uy=10√3sin(60∘)=10√3⋅√32=15m/s
The equations of motion for the ball can be described as:
- Horizontal motion: x=ux⋅t
- Vertical motion: y=uy⋅t−12gt2
The equation of the inclined plane can be derived from its angle:
- The slope of the incline is given by tan(30∘)=1√3.
- Thus, the equation of the inclined plane is y=1√3x.
We substitute x and y from the motion equations into the inclined plane equation:
uy⋅t−12gt2=1√3(ux⋅t)
Substituting the values:
15t−12⋅10t2=1√3(5√3t)
This simplifies to:
15t−5t2=5t
Rearranging gives:
10t−5t2=0
Factoring out t:
t(10−5t)=0
This gives us two solutions:
1. t=0 (the time of projection)
2. 10−5t=0⇒t=2s
The ball will hit the inclined plane after t=2s.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Relative Velocity In Two Dimensions23videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Kinematics Of Circular Motion26videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Projectile From A Height And Movingframe19videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration15videos
MOCK TEST
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
Similar Questions
A ball is projected from the foot of an inclined plane of inclination 30∘ at an angle 60∘ with the horizontal,with velocity 20√3ms−1 .The time after which the ball will strike the plane is
View SolutionIn the given figure , the angle of inclination of the inclined plane is 30∘. A particle is projected with horizontal velocity v0 from height H. Find the horizotnal velocity v0 (in m/s) so that the particle hits the inclined plane perpendicu lar .Given H=4m, g=10m/s2.
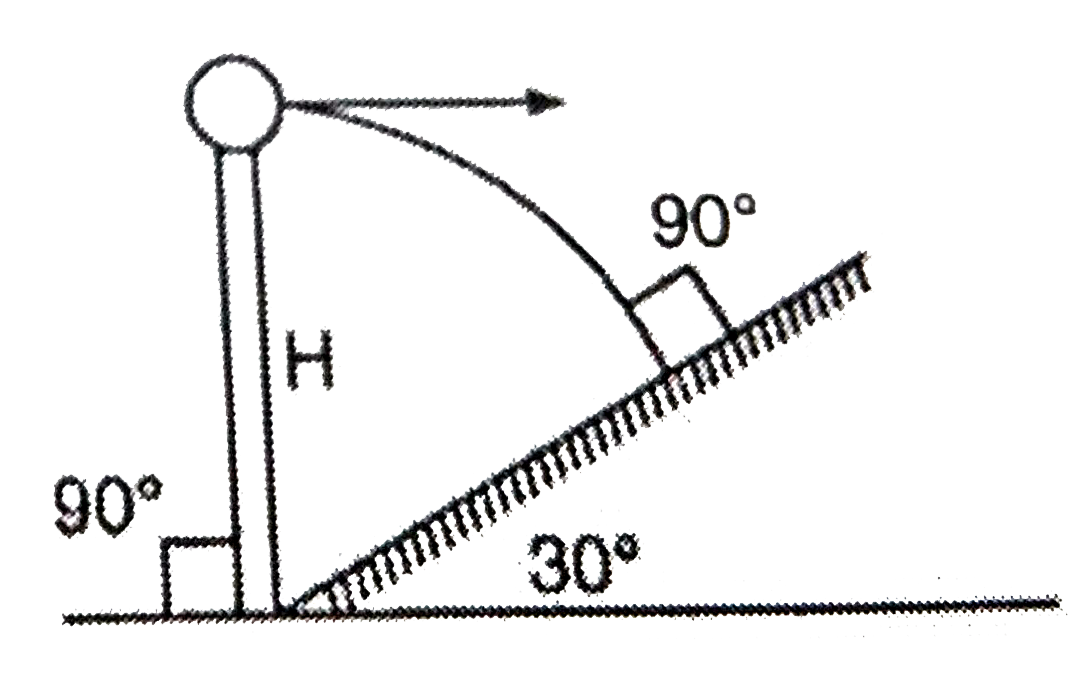 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
A12 mB60 mC120 mD600 m - Question 2 - Select One
A projectile is projected with speed u at an angle of 60∘ with horizontal from the foot of an inclined plane. If the projectile hits the inclined plane horizontally, the range on inclined plane will be.
Au2(√21)2gB3u24gCu22βD(√21)u28g - Question 3 - Select One
A ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time
 Av0√3gB2v0√3gCv0gD2√3v0g
Av0√3gB2v0√3gCv0gD2√3v0g
A bullet is fired from the bottom of the inclined plane at angle θ=37∘ with the inclined plane. The angle of incline is 30∘ with the horizontal. Find the
(a) position of the maximum height of the bullet from the inclined plane ,
(b) time of light ,
( c) range along the incline ,
(d) the value of θ at which the range will be maximum ,
( e) maximum range.View SolutionA hollow cylinder is rolling on an inclined plane, inclined at an angle of 30∘ to the horizontal. Its speed after travelling a distance of 10 m will be
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View SolutionIn figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 . View Solution
. View Solution

