A bullet moving with a speed of 200 m s−1 is absorbed by a wooden block of mass 1500 g suspended by a string . Caclulate the vertical height through which the block will rise . The mass of the bullet is 20 g .
To solve the problem of how high the wooden block will rise after being hit by the bullet, we will follow these steps:
Step 1: Convert the masses to kilograms
The mass of the bullet is given as 20 g and the mass of the block is 1500 g. We need to convert these masses into kilograms for standard SI units.
- Mass of the bullet, mb=20g=0.02kg
- Mass of the block, mB=1500g=1.5kg
Step 2: Calculate the initial momentum
The initial momentum of the system before the collision is given by the momentum of the bullet since the block is at rest.
Initial momentum=mb⋅vb=0.02kg⋅200m/s=4kg m/s
Step 3: Calculate the final velocity after the collision
Using the principle of conservation of momentum, the total momentum before the collision equals the total momentum after the collision.
Let v be the final velocity of the block and bullet together after the collision.
Initial momentum=Final momentum
4kg m/s=(mb+mB)⋅v
4=(0.02+1.5)⋅v
4=1.52⋅v
v=41.52≈2.63m/s
Step 4: Use the work-energy principle to find the height
According to the work-energy principle, the work done by the gravitational force will equal the change in kinetic energy.
The initial kinetic energy (KE) of the system just after the collision is:
KE=12(mb+mB)v2=12⋅1.52⋅(2.63)2
Calculating this:
KE=12⋅1.52⋅6.9169≈5.25J
The work done against gravity when the block rises to height h is given by:
Work=m⋅g⋅h=(mb+mB)⋅g⋅h
Setting the work done equal to the initial kinetic energy:
m⋅g⋅h=KE
1.52⋅9.81⋅h=5.25
h=5.251.52⋅9.81≈5.2514.9112≈0.352m
Final Answer
The vertical height through which the block will rise is approximately 0.352 meters.
---
The mass of the bullet is given as 20 g and the mass of the block is 1500 g. We need to convert these masses into kilograms for standard SI units.
- Mass of the block, mB=1500g=1.5kg
The initial momentum of the system before the collision is given by the momentum of the bullet since the block is at rest.
Using the principle of conservation of momentum, the total momentum before the collision equals the total momentum after the collision.
4kg m/s=(mb+mB)⋅v
4=(0.02+1.5)⋅v
4=1.52⋅v
v=41.52≈2.63m/s
According to the work-energy principle, the work done by the gravitational force will equal the change in kinetic energy.
1.52⋅9.81⋅h=5.25
h=5.251.52⋅9.81≈5.2514.9112≈0.352m
The vertical height through which the block will rise is approximately 0.352 meters.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Conceptual Questions20videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Tough & Tricky (PROBLEMS)15videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Chapter Practice Test16videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
WAVES
Similar Questions
A bullet of mass 10g travels horizontally with speed 100m/s and is absorbed by a wooden block of mass 900 g suspended by a string. Find the vertical height through which the block rises. Given g=10m/s2
View SolutionA bullet of mass 20 g moving horizontally at speed of 300 m/s is fired into wooden block of mas 500 suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
View Solution
Knowledge Check
- Question 1 - Select One
A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2 - Question 2 - Select One
A bullet of mass 10 gm moving with a horizontal velocity 100m/s passes through a wooden block of mass 100 gm. The block is resting on a smooth horizontal floor. After passing through the block the velocity of the bullet is 10m/s. the velocity of the emerging bullet with respect to the block is
A10m/sB9m/sC1m/sD5m/s - Question 3 - Select One
A bullet of mass 10gm moving with a horizontal velocity 100m/s passes through a wooden block of mass 100gm. The block is resting on a smooth horizontal floor. After passing through the block the velocity of the bullet is 10m/s the velocity of the emerging bullet with respect to the block is .
A10m/sB9m/sC1m/s.D5m/s
A bullet of mass 0.01 kg travelling at a speed of 500 m/s strikes a block of mass 2 kg, which is suspended by a string of length 5 m. The centre of gravity of the block is found to rise a vertical distance of 0.1 m. The speed of the bullet after it emerges from the block will be -
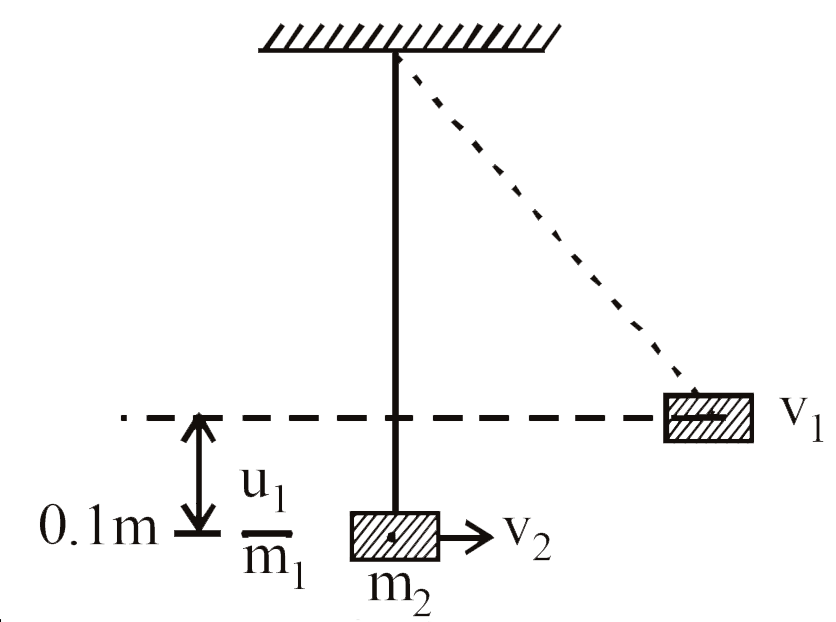 View Solution
View SolutionA bullet of mass 0.04 kg moving with a speed of 90ms−1 enters a heavy wooden block and is stooped after a distance of 60 cm . What is the average resistive force exerted by the block on the bullet ?
View SolutionA bullet of mass 0.06 kg moving with a speed of 90ms−1 enters a heavy wooden block and it stopped after a distance of 60 cm. What is the average resistive force exerted by the block on the bullet ?
View SolutionA bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
View SolutionA bullet of mass 10 g moving horizontally with a velocity of 400ms−1 strikes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5 m. As a result, the centre of gravity of the block is found to rise a vertical distance of 10 cm. The speed of the bullet after it emerges out horizontally from the block will be
View Solution

