A bullet of mass 10g travels horizontally with speed 100m/s and is absorbed by a wooden block of mass 900 g suspended by a string. Find the vertical height through which the block rises. Given g=10m/s2
To solve the problem step by step, we will follow these steps:
Step 1: Convert the masses to kilograms
The mass of the bullet (m) is given as 10 grams, and the mass of the wooden block (M) is given as 900 grams. We need to convert these masses into kilograms for our calculations.
m=10g=101000kg=0.01kg
M=900g=9001000kg=0.9kg
Step 2: Calculate the initial momentum
The bullet is traveling with a speed of 100 m/s. The initial momentum (p_initial) of the bullet can be calculated using the formula:
pinitial=m⋅U1=0.01kg⋅100m/s=1kg m/s
Step 3: Apply conservation of momentum
When the bullet is absorbed by the wooden block, the total momentum before the collision is equal to the total momentum after the collision. Let V be the common velocity after the collision.
pinitial=pfinal⟹1kg m/s=(m+M)⋅V
1=(0.01+0.9)⋅V⟹1=0.91⋅V
V=10.91≈1.1m/s
Step 4: Calculate the kinetic energy after the collision
The kinetic energy (KE) of the combined system (bullet + block) after the collision can be calculated using the formula:
KE=12(m+M)V2
KE=12(0.01+0.9)(1.1)2=12(0.91)(1.21)≈0.55J
Step 5: Set up the potential energy equation
As the block rises, the kinetic energy will be converted into potential energy (PE). The potential energy gained when the block rises to height h is given by:
PE=(m+M)gh
Setting the kinetic energy equal to the potential energy:
KE=PE⟹0.55=(0.91)(10)h
0.55=9.1h
h=0.559.1≈0.0604m
Step 6: Convert height to centimeters
To express the height in centimeters:
h≈0.0604m=6.04cm
Final Answer
The vertical height through which the block rises is approximately 6.04 cm.
---
The mass of the bullet (m) is given as 10 grams, and the mass of the wooden block (M) is given as 900 grams. We need to convert these masses into kilograms for our calculations.
M=900g=9001000kg=0.9kg
The bullet is traveling with a speed of 100 m/s. The initial momentum (p_initial) of the bullet can be calculated using the formula:
When the bullet is absorbed by the wooden block, the total momentum before the collision is equal to the total momentum after the collision. Let V be the common velocity after the collision.
1=(0.01+0.9)⋅V⟹1=0.91⋅V
V=10.91≈1.1m/s
The kinetic energy (KE) of the combined system (bullet + block) after the collision can be calculated using the formula:
KE=12(0.01+0.9)(1.1)2=12(0.91)(1.21)≈0.55J
As the block rises, the kinetic energy will be converted into potential energy (PE). The potential energy gained when the block rises to height h is given by:
Setting the kinetic energy equal to the potential energy:
0.55=9.1h
h=0.559.1≈0.0604m
To express the height in centimeters:
The vertical height through which the block rises is approximately 6.04 cm.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Conceptual Problems27videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.54videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Curiosity questions2videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
A bullet moving with a speed of 200 m s−1 is absorbed by a wooden block of mass 1500 g suspended by a string . Caclulate the vertical height through which the block will rise . The mass of the bullet is 20 g .
View SolutionA bullet of mass 20 g moving horizontally at speed of 300 m/s is fired into wooden block of mas 500 suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
View Solution
Knowledge Check
- Question 1 - Select One
A bullet of mass 10 gm moving with a horizontal velocity 100m/s passes through a wooden block of mass 100 gm. The block is resting on a smooth horizontal floor. After passing through the block the velocity of the bullet is 10m/s. the velocity of the emerging bullet with respect to the block is
A10m/sB9m/sC1m/sD5m/s - Question 2 - Select One
A bullet of mass 10gm moving with a horizontal velocity 100m/s passes through a wooden block of mass 100gm. The block is resting on a smooth horizontal floor. After passing through the block the velocity of the bullet is 10m/s the velocity of the emerging bullet with respect to the block is .
A10m/sB9m/sC1m/s.D5m/s - Question 3 - Select One
A bullet of mass m moving with a horizontal velocity u strikes a stationary wooden block of mass M suspended by a string of length L = 50 cm. The bullet emerges out of the block with speed u4. If M = 6 m, minimum value of u so that the block can complete the vertical circle (take, g = 10 ms−2)
A10 ms−1B20 ms−1C30 ms−1D40 ms−1
A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bulet emerges with speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction cioefficient between the block and the surface figure.
 View Solution
View SolutionA wooden block of mass 0.9kg is suspended from the ceiling of a room by thin wires. A bullet of mass 0.1kg moving horizontally with a speed of 10ms−1 strikes the block and sticks to it. What is the height to which the block rises ? Take g=10ms−2:
View SolutionA bullet of mass m moving horizontally with speed u strikes a suspended wooden block of mass M and gets embedded into it. If block rises to height L2 where L is length of string with which wooden block is connected.The initial velocity(u) of bullet is
View SolutionA bullet of mass 0.01 kg travelling at a speed of 500 m/s strikes a block of mass 2 kg, which is suspended by a string of length 5 m. The centre of gravity of the block is found to rise a vertical distance of 0.1 m. The speed of the bullet after it emerges from the block will be -
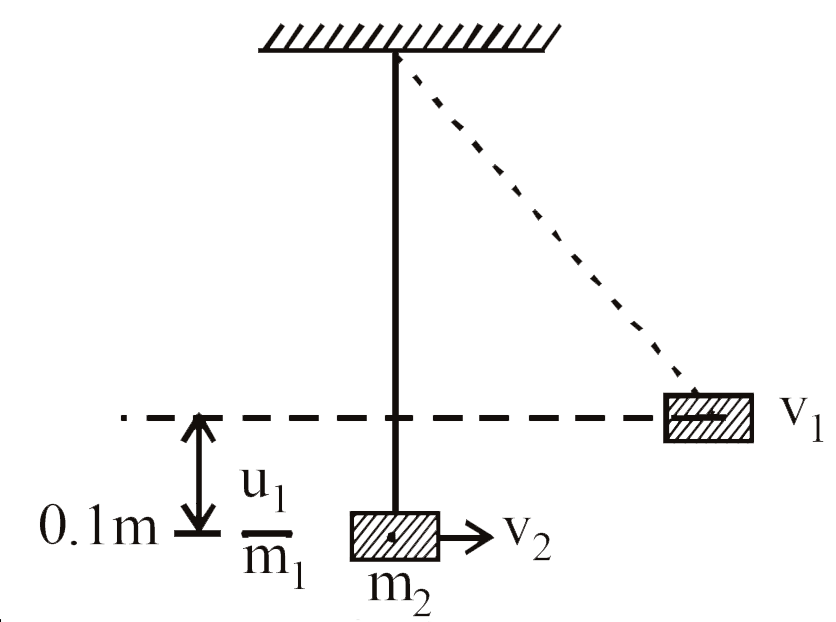 View Solution
View SolutionA bullet of mass 10g moving horizontally with a speed of 400m/s a block of mass 390g and remains in it. The block slides 10m on rough surface before coming to rest. The friction coefficient is
View Solution

