A bullet of mass 10 g is fired horizontally into a 4 kg wooden block resting on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.25. The bullet is embadded the block and the combination moves a distance of 20 m before coming to rest. Find the speed of the bullet just before striking the block. (g=10m/s2)
To find the speed of the bullet just before striking the block, we can follow these steps:
Step 1: Understand the problem
We have a bullet of mass mb=10g=0.01kg fired into a wooden block of mass mB=4kg. The bullet embeds itself into the block, and they move together after the collision. The coefficient of kinetic friction between the block and the surface is μ=0.25. The block and bullet combination moves a distance of s=20m before coming to rest.
Step 2: Calculate the deceleration due to friction
The frictional force Ff acting on the block and bullet combination can be calculated as:
Ff=μ⋅(mB+mb)⋅g
Where g=10m/s2.
Calculating the total mass:
mB+mb=4kg+0.01kg=4.01kg
Now substituting the values:
Ff=0.25⋅4.01⋅10=10.025N
The acceleration (deceleration in this case) a can be found using Newton's second law F=ma:
a=FfmB+mb=10.0254.01≈2.5m/s2
Step 3: Use the equations of motion
The combination comes to rest after moving a distance of s=20m. Using the equation of motion:
v2=u2+2as
Where:
- v=0 (final velocity),
- u is the initial velocity of the combination after the collision,
- a=−2.5m/s2 (deceleration),
- s=20m.
Rearranging the equation:
0=u2−2⋅2.5⋅20
u2=100
u=10m/s
Step 4: Apply conservation of momentum
Before the collision, the momentum is given by the bullet's momentum since the block is at rest:
pinitial=mb⋅v
After the collision, the momentum is:
pfinal=(mB+mb)⋅u
Setting the initial momentum equal to the final momentum:
mb⋅v=(mB+mb)⋅u
Substituting the known values:
0.01⋅v=4.01⋅10
0.01⋅v=40.1
v=40.10.01=4010m/s
Final Answer
The speed of the bullet just before striking the block is approximately 4010 m/s.
---
We have a bullet of mass mb=10g=0.01kg fired into a wooden block of mass mB=4kg. The bullet embeds itself into the block, and they move together after the collision. The coefficient of kinetic friction between the block and the surface is μ=0.25. The block and bullet combination moves a distance of s=20m before coming to rest.
The frictional force Ff acting on the block and bullet combination can be calculated as:
Ff=μ⋅(mB+mb)⋅g
Where g=10m/s2.
mB+mb=4kg+0.01kg=4.01kg
Ff=0.25⋅4.01⋅10=10.025N
a=FfmB+mb=10.0254.01≈2.5m/s2
The combination comes to rest after moving a distance of s=20m. Using the equation of motion:
v2=u2+2as
Where:
- v=0 (final velocity),
- u is the initial velocity of the combination after the collision,
- a=−2.5m/s2 (deceleration),
- s=20m.
0=u2−2⋅2.5⋅20
u2=100
u=10m/s
Before the collision, the momentum is given by the bullet's momentum since the block is at rest:
pinitial=mb⋅v
pfinal=(mB+mb)⋅u
mb⋅v=(mB+mb)⋅u
Substituting the known values:
0.01⋅v=4.01⋅10
0.01⋅v=40.1
v=40.10.01=4010m/s
The speed of the bullet just before striking the block is approximately 4010 m/s.
Topper's Solved these Questions
Similar Questions
A block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View Solution
Knowledge Check
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20NA block of mass 2 kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between block and surface is 0.1. The work done by the applied force in 10 s is (Take g=10ms−2)
A200JB−200JC600 JD−600J
A wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View SolutionA horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. the weight of the block is (g=10m/s2)

View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and g=10ms−2 The frictional force on the block is
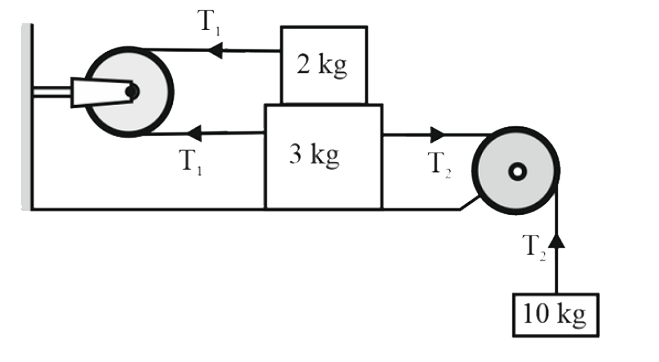
View SolutionCoefficient of kinetic friction between 3 kg and 2 kg block is 0.25. The horizontal table surface is smooth. Find the acceleration (in S.I. unit) of the block of mass 10 kg.
View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View SolutionA 5 kg block rests on a horizontal surface. Which of the following option is incorrect? (g=10ms)

View Solution
