A bullet of mass m hits a wooden block of mass M, suspended by a string of length l, and gets embedded in it. If the velocity of the bullet is v, find the angular displacement of the block.
Let the velocity of the block -bullet system after impact be V and the angular displacement be θ [Fig.1.48].

From the law of conservation of momentum,
mv=(M+m)Vor,V=mvM+m
Kinetic energy of the block -bullet system at position A
=12(M+m)V2
=12(M+m)×m2v2(M+m)2
=m2v22(M+m)
Potential energy of the system at B
=(M+m)g⋅AC
=(M+m)g[OA−OC]
=(M+m)g(l−lcosθ)=(M+m)gl(1−cosθ)
From the law of conservation of energy,
12m2v2M+m=(M+m)gl(1−cosθ)
or, 1−cosθ=12m2v2(M+m)2gl
or,2sin2θ2=12(mvM+m)2×1gl
or,sinθ2=mv2(M+m)√glor,θ2=sin−1[mv2(M+m)√gl]
∴θ=2sin−1[mv2(M+m)√gl].
Topper's Solved these Questions
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - SECTION RELATED QUESTIONS
24 Videos
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
38 Videos
- WBCHSE QUESTION PAPER -2019BOOK - CHHAYA PUBLICATIONCHAPTER - WBCHSE QUESTION PAPER -2019EXERCISE - SECTION - II ( GROUP -D)
10 Videos
Similar Questions
A bullet of mass m hits a target of mass M hanging by a string and gets embedded in it. If the block rises to a height h as a result of this collision, the velocity of the bullet before collision is
View SolutionA bullet of mass 0.01 kg travelling at a speed of 500 m/s strikes a block of mass 2 kg, which is suspended by a string of length 5 m. The centre of gravity of the block is found to rise a vertical distance of 0.1 m. The speed of the bullet after it emerges from the block will be -
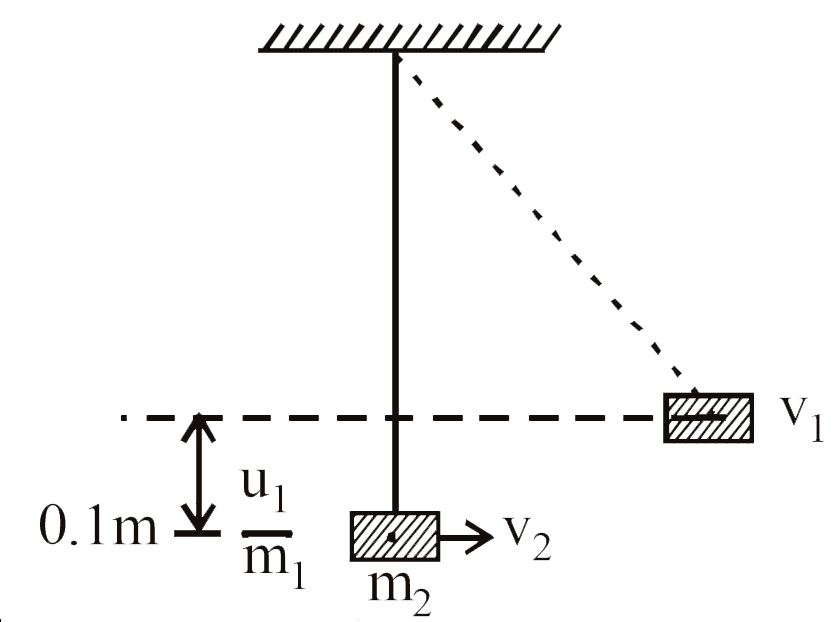
View Solution
Knowledge Check
A bullet of mass m hits a target of mass M hanging by a string and gets embeded in it. If the block rises to a height h as a result of this collision, the velocity of the bullet before collision is
Av=√2ghBv=√2gh[1+mM]Cv=√2gh[1+Mm]Dv=√2gh[1−mM]A bullet of mass 'x' moves with a velocity y, hits a wooden block of mass z at rest and gets embedded in it. After collision, the wooden block and bullet moves with a velocity
Axx+zyBx+yxyCzx+yyDx+yzyA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A12mv2×m(m+M)B12mv2×M(m+M)C12mv2×(M+m)mD12Mv2×m(m+M)
A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m is fired into a block of wood of mass M which hangs on the end of pendulum and gets embedded into it. When the bullet strikes with maximum rise R. Then, the velocity of the bullet is given by
View SolutionA bullet of mass 20 g hits a block of mass 1.98 kg suspended from a massless string of length 100 cm and sticks to it. The bullet flies down at an angle of 30º to the horizontal with a velocity of 200 m/s. Through what height the block will rise-
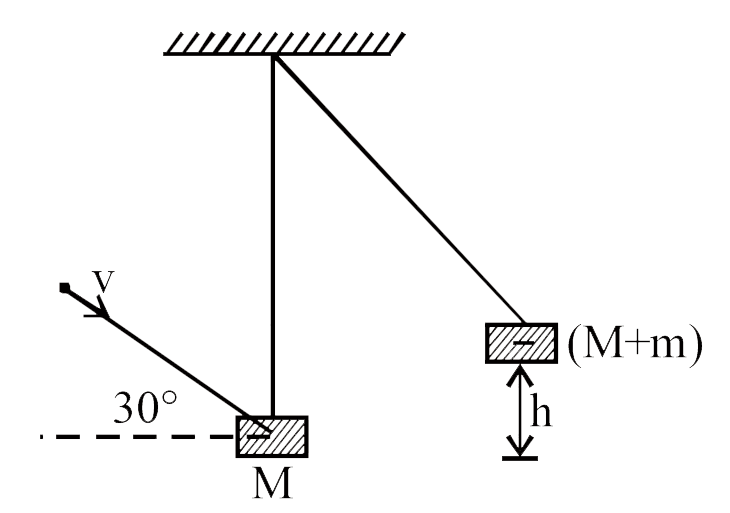
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m is fired into a block of wood of mass M which hangs on the end of pendulum and gets embedded into it. When the bullet strikes with maximum rise R. Then, the velocity of the bullet is given by
View Solution
