A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
12mMu2
12(m+M)u2
m2v22(m+M)
(m+M2mM)u2
The correct Answer is:C
To solve the problem, we need to find the kinetic energy of the composite block formed when a bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it.
1. Identify the Initial Conditions:
- Mass of the bullet, m
- Velocity of the bullet, v
- Mass of the block, M (initially at rest)
2. Apply the Law of Conservation of Momentum:
The total momentum before the collision must equal the total momentum after the collision.
Initial Momentum=Final Momentum
Before the collision, the momentum is:
pinitial=mv+M⋅0=mv
After the collision, the bullet gets embedded in the block, and they move together with a common velocity U:
pfinal=(m+M)U
Setting these equal gives:
mv=(m+M)U
3. Solve for the Final Velocity U:
Rearranging the equation to solve for U:
U=mvm+M
4. Calculate the Kinetic Energy of the Composite Block:
The kinetic energy KE of the composite block is given by:
KE=12(m+M)U2
Substituting U from the previous step:
KE=12(m+M)(mvm+M)2
5. Simplify the Expression:
KE=12(m+M)⋅m2v2(m+M)2
KE=12⋅m2v2m+M
6. Final Result:
The kinetic energy of the composite block after the collision is:
KE=m2v22(m+M)
- Mass of the bullet, m
- Velocity of the bullet, v
- Mass of the block, M (initially at rest)
The total momentum before the collision must equal the total momentum after the collision.
Initial Momentum=Final Momentum
Before the collision, the momentum is:
pinitial=mv+M⋅0=mv
After the collision, the bullet gets embedded in the block, and they move together with a common velocity U:
pfinal=(m+M)U
Setting these equal gives:
mv=(m+M)U
Rearranging the equation to solve for U:
U=mvm+M
The kinetic energy KE of the composite block is given by:
KE=12(m+M)U2
Substituting U from the previous step:
KE=12(m+M)(mvm+M)2
KE=12(m+M)⋅m2v2(m+M)2
KE=12⋅m2v2m+M
The kinetic energy of the composite block after the collision is:
KE=m2v22(m+M)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
35 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - C)
80 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE
37 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A body of mass a moving with a velocity b strikes a body of mass c and gets embedded into it. The velocity of the systems after collision is
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View Solution
Knowledge Check
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
A rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod

View SolutionTwo blocks of masses m and 3m are connected by an inextensible string and the string passes over a fixed pulley which is massless and frictionless. A bullet of mass m moving with a velocity 'u' hits the hanging block of mass 'm' and gets exbedded in it. Find the height through which block A rises after the collision.
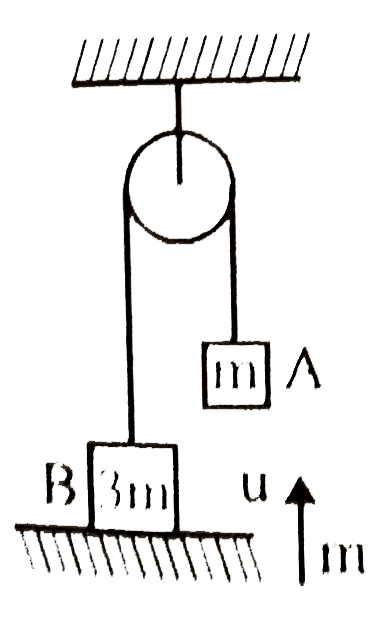
View SolutionA circular wooden hoop of mass m and radius R rests fiat on a frictionless surface. A bullet, also of mass m and moving with a velocity v, strikes the hoop and gets embedded in it. The thickness of the hoop is much smaller than R. Find the angular velocity with which the system rotates in after the bullet strikes the hoop.
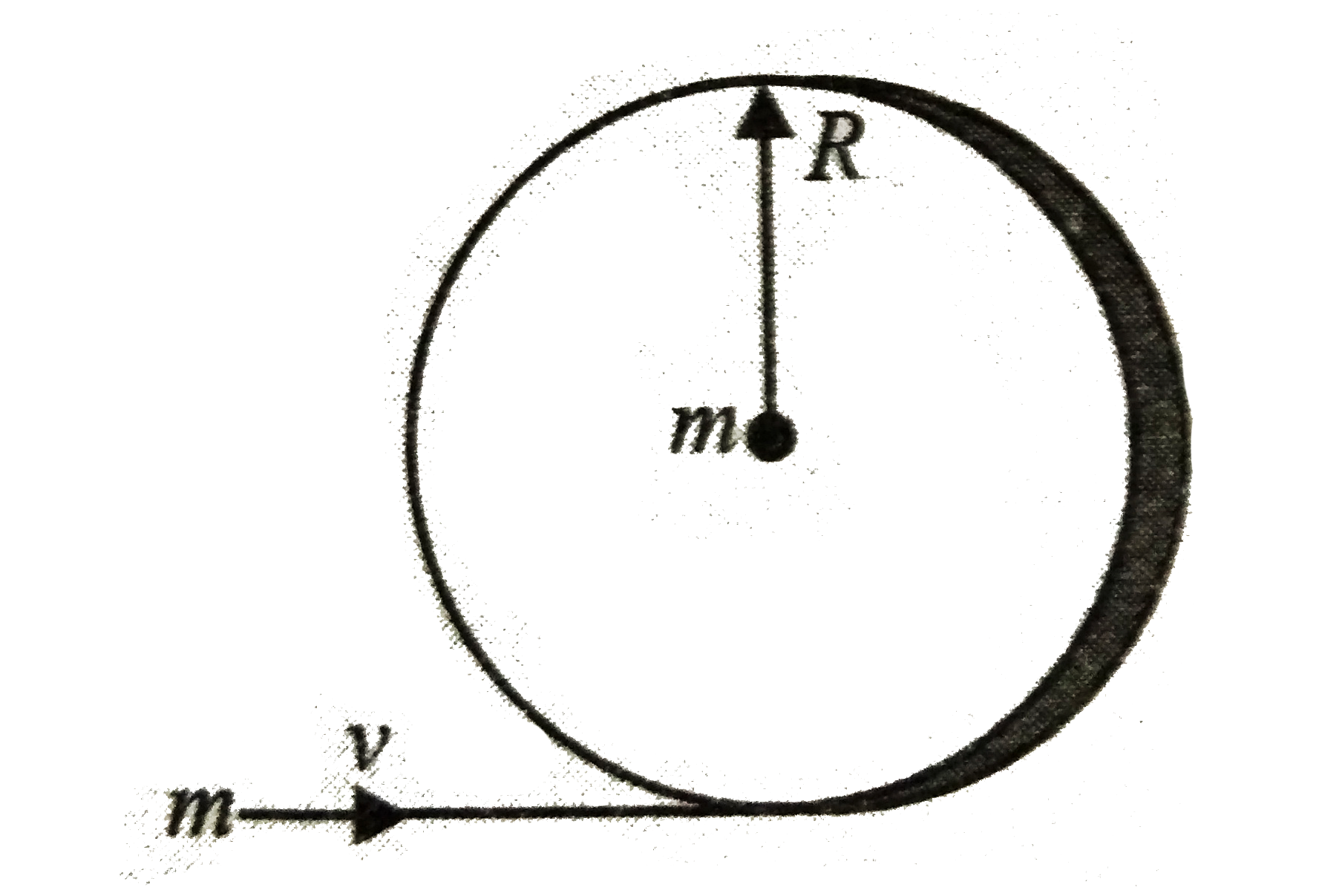
View SolutionA system of two blocks A and B are connected by an inextensible massless string as shown in Fig. The pulley is massless and frictionless. Initially, the system is at rest. A bullet of mass m moving with a velocity u as shown hits block If and gets embedded into it. The impulse imparted by tension force to the block of mass 3m is

View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionIn the given diagram a 0.1 kg bullet moving with speed 20 m/sec strikes 1.9kg mass and get embedded in it. find the kinetic energy of the mass with which it will strikes the ground is

View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View Solution
