A cannon and a target are 5.10Km apart and located at the same level. How soon will the shell launched with the initial velocity 240m/s reach the target in the absence of air drag?
Here v0=240ms−1,R=5.10km=5100m
g=9.8ms−2,α=? R=v202αg
sin2α=Rgv20 ⇒α=30∘or60∘
Using =T=2v0sinαg
When α=30∘,T1=2×240×0.59.8=24.5s
When α=60∘T2=2×240×0.8679.8=42.41s
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)
25 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)
10 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
Two balls of equal masses are thrown upwards, along the same vertical direction at an interval of 2 seconds, with the same initial velocity of 40m/s. Then these collide at a height of (Take g=10m/s2).
View SolutionA cannon of mass 5m (including a shell of mass m) is at rest on a smooth horizontal ground, fires the shell with its barrel at an angle θ with the horizontal at a velocity u relative to cannon. Find the horizontal distance of the point where shell strikes the ground from the initial position of the cannon :-
View SolutionA cannon of mass 1000kg located at the base of an inclined plane fires a shell of mass 50kg in horizontal direction with velocity 180km/h. The angle of inclination of the inclined plane with the horizontal is 45∘. The coefficient of friction between the cannon and inclined plane is 0.5. The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
View SolutionA bullet of mass 20 g leaves a riffle at an initial speed 100 m/s and strikes a target at the same level with speed 50 m/s. The amount of work done by the resistance of air will be
View SolutionAn observer having a gun observes a remotely controlled balloon. When he first noticed the balloon, it was at an altitude of 800m and moving vertically upward at a constant velocity of 5m/s. The horizontal displacement of balloon from the observer is 1600m. Shells fired from the gun have an initial velocity of 400m/s at a fixed angle θ(sinθ=3/5and cosθ=4/5). The observer having gun waits ( for some time after observing the balloon ) and fires so as to destroy the balloon. Assume g=10m/s2. Neglect air resistance.
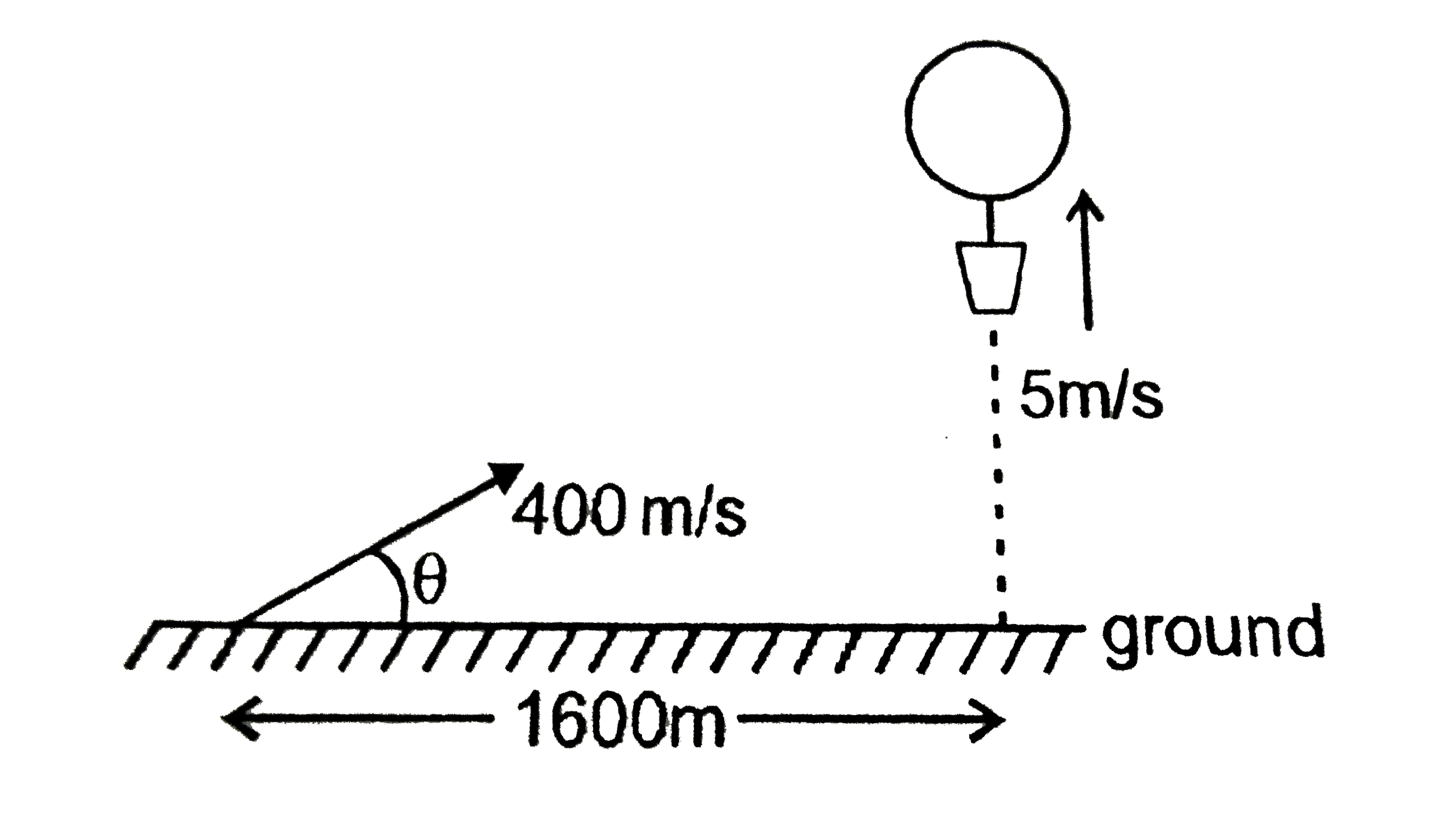
The altitude of the collosion above ground level is
View SolutionAn observer having a gun observes a remotely controlled balloon. When he first noticed the balloon, it was at an altitude of 800m and moving vertically upward at a constant velocity of 5m/s. The horizontal displacement of balloon from the observer is 1600m. Shells fired from the gun have an initial velocity of 400m/s at a fixed angle θ(sinθ=3/5and cosθ=4/5). The observer having gun waits ( for some time after observing the balloon ) and fires so as to destroy the balloon. Assume g=10m/s2. Neglect air resistance.

The flight time of the shell before it strikes the balloon is
View SolutionA car P is moving with a uniform speed 5√3m/s towards a carriage of mass 9 kg at rest kept on the rails at a point B as shown in the figure. The height AC is 120 m. Cannon balls of 1 kg are fired from the car with an initial velocity 100 m/s with respect to the car at an angle 30∘ with the horizontal.

The first cannon ball hits the stationary carriage after a time t0 and sticks to it. Determine t0. (in sec)
View SolutionA projectile is fired vertically from the earth's surface with an initial speed of 10km/s. Neglecting air drag, how high above the surface of earth will it go?
View SolutionA bullet of mass 10g leaves a rifle at an intial velocity of 1000m/s and strikes the earth at the same level with a velocity of 500m/s. The work done in joule to overcome the resistance of air will be
View SolutionA projectille covers a horizontal distance of 6 m, when it reaches 10 m above the level of projection, how farther should if travel horizontally to reach back the same height , if its horizontal range is 20 m ?
View Solution
