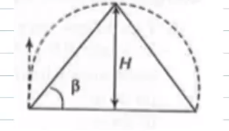
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If be the base angles and the angle of projection, prove that .
Step by step video & image solution for A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If alpha and beta be the base angles and theta the angle of projection, prove that tan theta = tan alpha + tan beta . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:NUMERICAL EXERCISE (LEVEL -2)
Explore 19 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-3 (Circular Motion)
Explore 7 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
Similar Questions
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30∘and60∘ be the base angles and θ the angle of projection then tanθ is
View SolutionIf cosθ=cosα−cosβ1−cosαcosβ,prove that tanθ2=±tanα2cotβ2.
View SolutionIf αandβ are roots of the equation acosθ+bsinθ=c, then find the value of tan(α+β).
View SolutionA shell fired from the base of a mountain just clears it. If α is the angle of projection, then the angular elevation of the summit β is
View SolutionIf α and β are acute such that α+β and α−β satisfy the equation tan2θ−4tanθ+1=0, then (α,β) =
View Solutionαandβ are acute angles and cos2α=3cos2β−13−cos2β then tanαcotβ=
View SolutionTwo particles are projected at the same instant from the same point at inclinations α and β to the horizontal. If they simultaneously hit the top and bottom of a vertical pole subtending angle θ at the point of projection , find (tanα−tanβ).
View SolutionIf tanβ=cosθtanα, then prove that tan2θ2=sin(α−β)sin(α+β).
View SolutionTwo parallel straight lines are inclined to the horizon at an angle ∝. A particle is projected from a point mid way between them so as to graze one of the lines and strikes the other at right angle. Show that if θ is the angle between the direction of projection and either of lines, then tanθ=(√2−1)cot∝.
View SolutionA train travelling on one of two intersecting railway lines, subtends at a certain station on the other line, an/ angle α when the front of the carriage reaches the junction and an angle β when the end of the carriage reaches it. Then, the two lines are inclined to each other at an angle θ, show that 2cotθ=cotα−cotβcotα+cotβ
View Solution
