A capacitor is charged using an external battery with a resistance x in series. The dashed line showns the variation of In I with respect to time. If the resistance is changed to 2x, the new graph will be
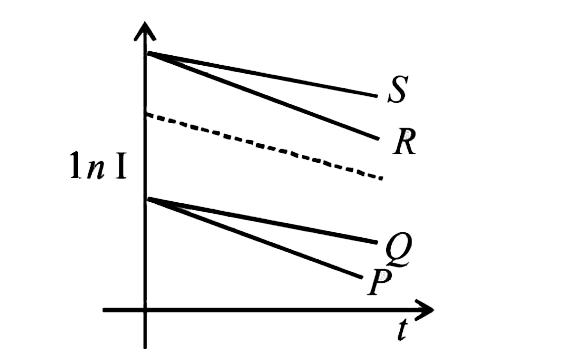
P
Q
R
S
The correct Answer is:B
b. The current in RC circuit is given by I=I0e−t/RC
or 1nI=1nI0−tRC=−tRC+1NI0
=(−tRC)+1nE0R
On comparing with y=mx+C, we get
Intercept =1nE0Randslope=−1RC
When R is changed to 2R, then slope decreases in magnitude.
New graph is Q.
Similar Questions
There is no resistance in the capacitive circuit shown. Then charge on the capacitor at an time t
 View Solution
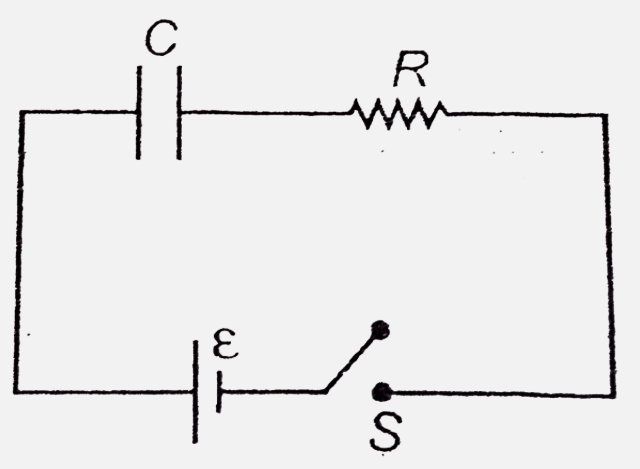
View SolutionAn uncharged capacitor is connected to an ideal battery through a resistance R and a switch S. Initially the switch is open . At an instant, the switch is closed . Taking this instant as t=0, which of the following graphs represent correct variation of the quantity taken along y -axis with time ?
 View Solution
View SolutionA capacitor C is connected to the two equal resistances as shown in fig. What is the ratio of the time constant during charging and discharging of the capacitance?
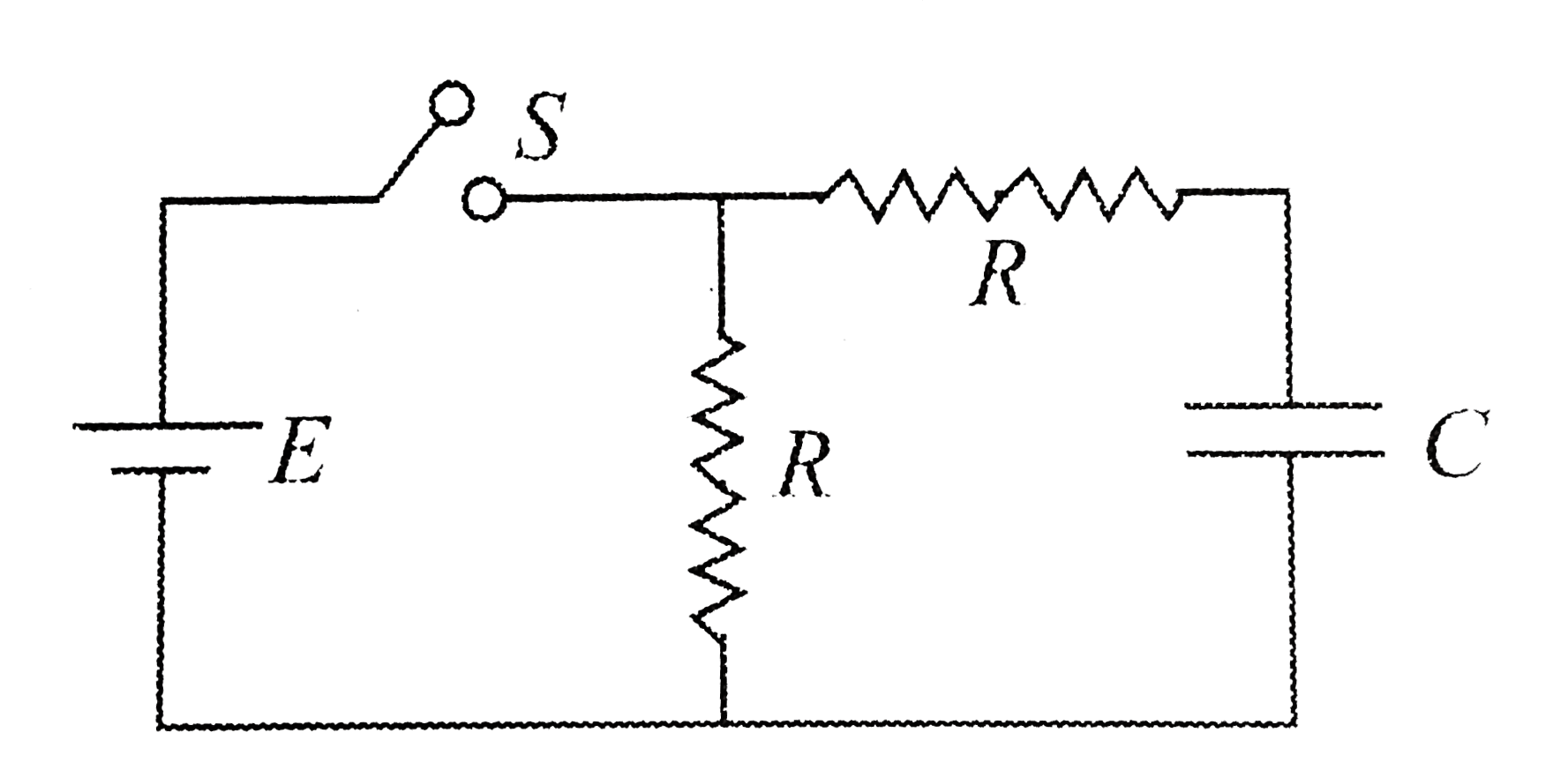 View Solution
View SolutionTwo capacitors of capacitance 2μF and 3μF respectively are charged to potential difference 20 V and 40 V respectively. Now the capacitors are connected in series with a resistance such that the positively charged plate of one capacitor is connected to the positively charged plate of the other. The initial current through the resistance is I0. The potential difference across the 2μF capacitor at the instant the current has reduced to I02 is_______ V.
View SolutionIf an uncharged capacitor is charged by connecting it with an ideal battery and a resistance R as shown. Then heat generated in resistor R by the time capacitor stores energy 18CV2 is :
 View Solution
View SolutionA 2μF capacitor that was initially uncharged is connected to a battery of EMF 100V and a resistance and the switch is closed. The heat generated in the resistance until the capacitor becomes fully charged is (in mJ):
View SolutionA capacitor of capacity 1μF is connected in a closed series circuit with a resistance or 107 ohms, an open key and a cell of 2 V with negligible internal resistance :
(i) When the key is switched on at time t=0, find,
(a) The time constant for the circuit.
(b) The charge on the capacitor at steady state.
(c) Time taken to deposit charge equal to half of charge that will deposit at steady state.
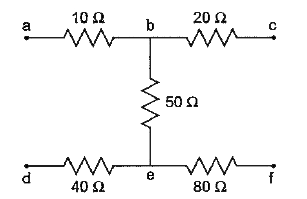
(ii) If after completely charging the capacitor, the cell is shorted by zero resistance at time t=0, find the charge on the capacitor at t=50 s. (Given : e−5=6.73×10−3,ln2=0.693)View SolutionThe equivalent resistance between points a and f of the network shown in figure below is
 View Solution
View SolutionAn Uncharged capacitor C is connected to a battery through a resistance R. Show that by the time the capacitor gets fully charged, the energy dissipated in R is the same as the energy stored in C.
View SolutionA capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets
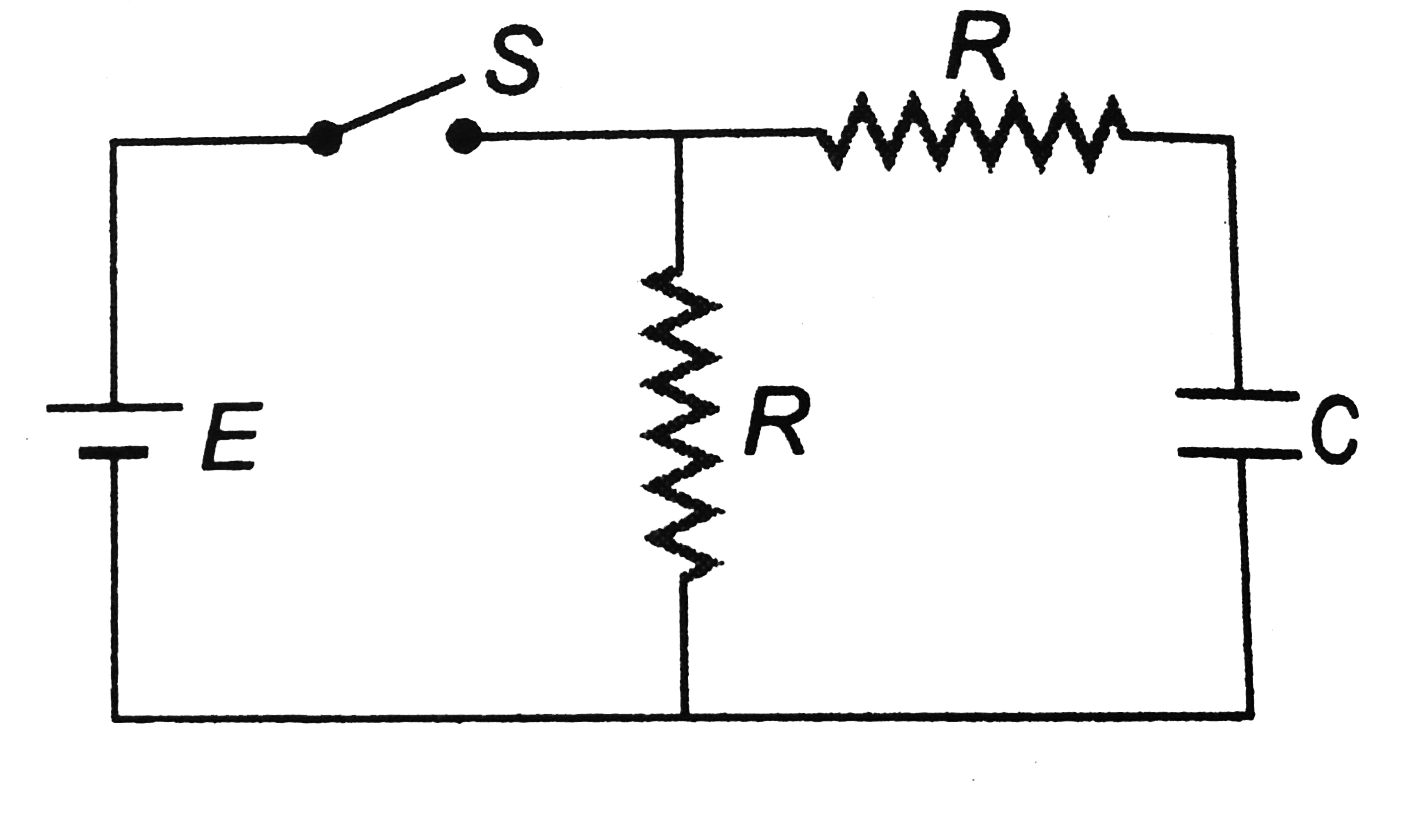
i. At the time of charging of capacitor time constant of the circuit is CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CRView Solution

