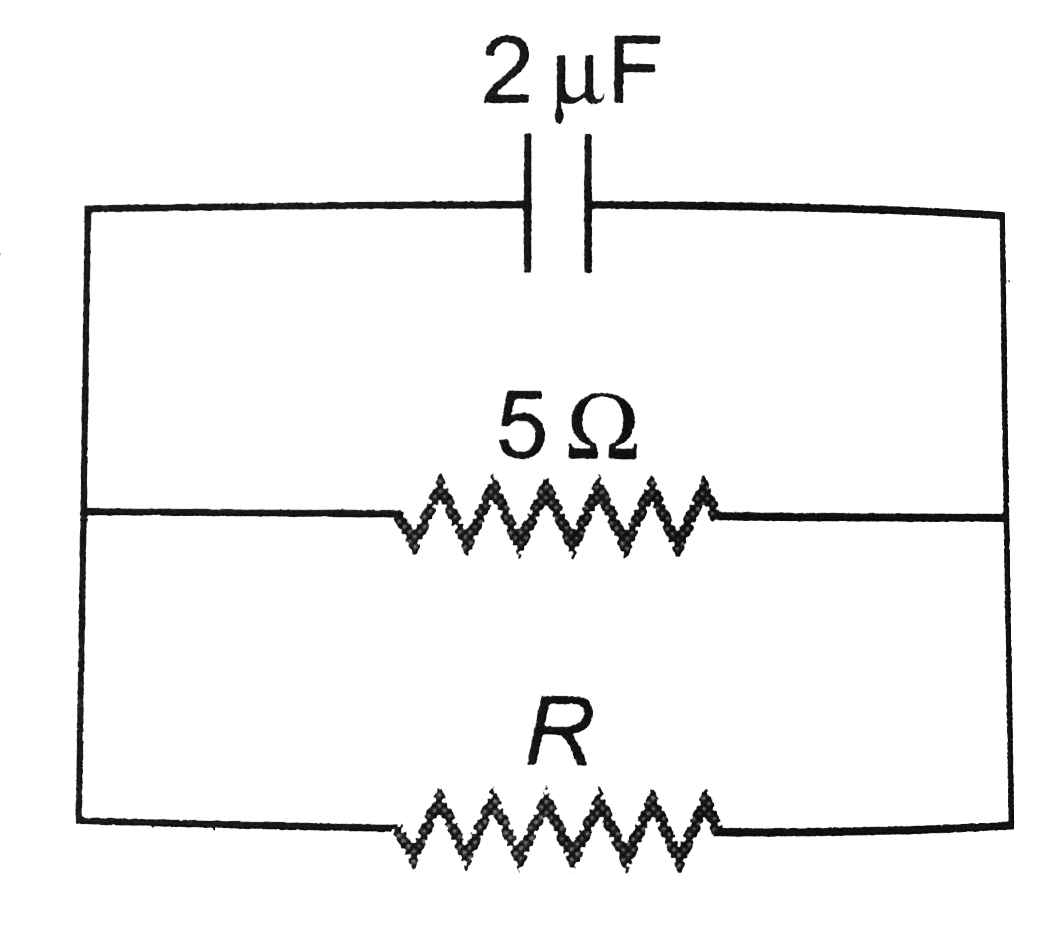
A capacitor of capacitance 2muF is charged to a potential difference o

A capacitor of capacitance C is charged to a potential difference $V_{0}$ . The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance $C_{x}$ . The potential difference across the combination is V. The value of $C_{x}$ should be
A $\frac{C (V_{0} - V)}{V}$
B $\frac{C (V - V_{0})}{V}$
C $\frac{C V}{V_{0}}$
D $\frac{C V_{0}}{V}$
An ideal capacitor of capacitance $0.2 μ F$ is charged to a potential difference of $10 V$ . The charging battery is than disconnected. The capacitor is then connected to an ideal inductor of self inductance $0.5 m H$ . The current at a time when the potential difference across the capacitor is $5 V$ is :
A $0.34 A$
B $0.17 A$
C $0.25 A$
D $0.15 A$
A capacitor of capacitance of $2 μ F$ is charged to a potential difference of $200 V$ , after disconnecting from the battery, it is connected in parallel with another uncharged capacitor. The final common potential is $20 V$ then the capacitance of second capacitor is :
A $2 μ F$
B $4 μ F$
C $18 μ F$
D $16 μ F$

The correct Answer is:C