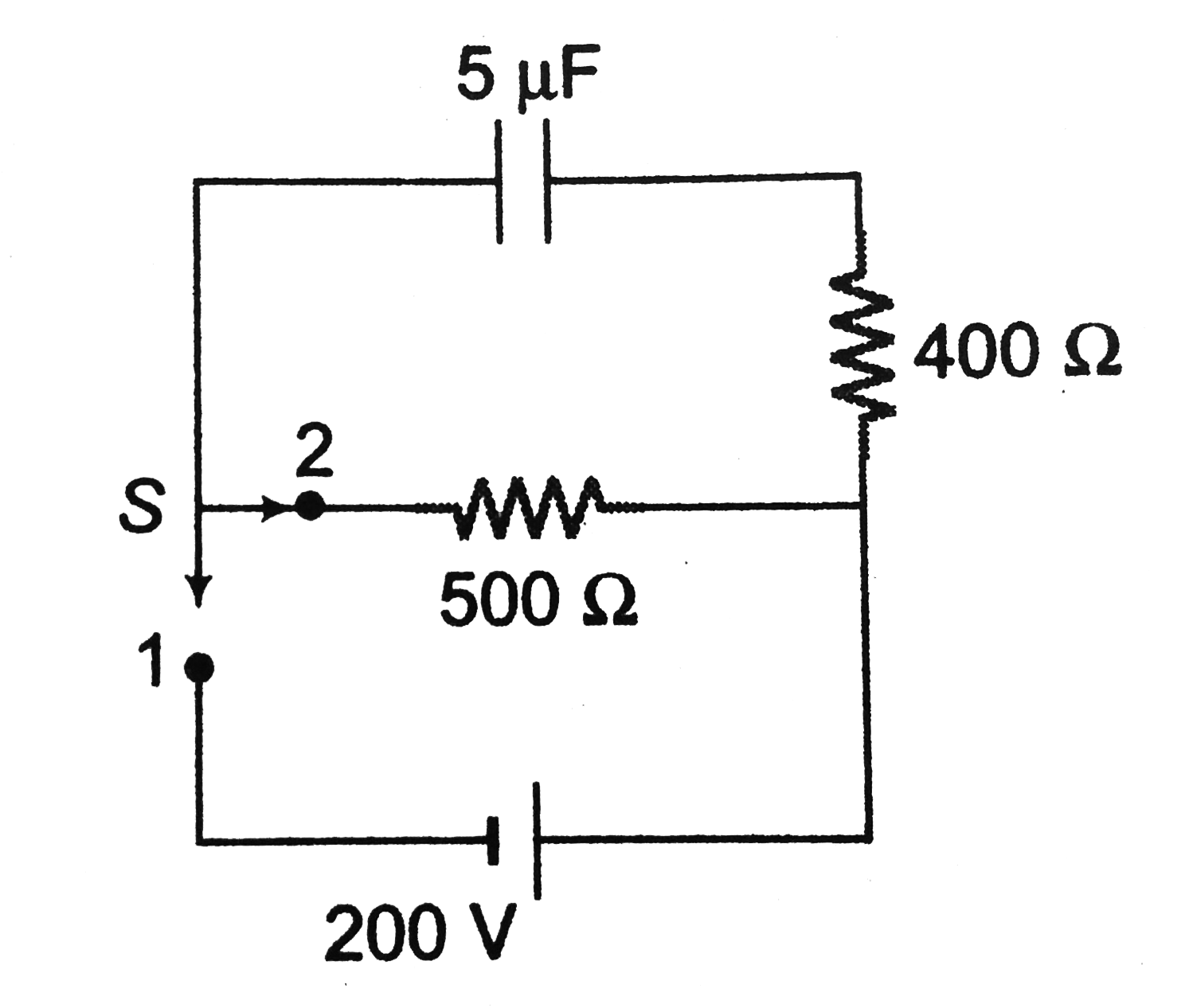
A capacitor of capacitance C=5.00μF is connected to a source of constant emfξ=200V (Fig). Then the swich Sw was thrown over from contact 1 to conatact 2. Find the amount of heat generated in a resistance R1=500Ω if R2=300Ω

When switch 1 is closed maximum charge accumulaated on the capacitor,
qmax=Cξ ......(1)
and when switch 2 is closed, at any arbitary instant of time,
(R1+R2)(−dqdt)=q/C,
because capacitor is discharging.
or, ∫qqmax1q=−1(R1+R2)C∫t0dt
Intergrating, we get
In qqmaxe=−t(R1+R2)C or, q=qmaxe=−t(R1+R2)C ....(2)
Differentiating with respect to time,
i(f)=dqdt=qmaxe−t(R1+R2)C(−1(R1+R2)C)
or, i(t)=Cξ(R1+R2)Ce−t(R1+R2)C
Negative sign is ignored, as we are not interested in the direction of the current.
thus, i(t)=ξ(R1+R2)e−1(R1+R2)C ....(3)
When the swich (Sw) is at the position 1, the charge (maximum) accumalted on the capacitor is,
q=Cξ
When teh Sw is thown to position 2, the capacitor starts discharging and as a result the electric energy stored turns into heat energy tho' the resistors R1 and R2 (during a very long interval of time). Thus from the energy conservation, the total heat liberated tho' the resistors.
H=Ui=q22C=12Cξ2
During the process of discharging of the capacitor, the current tho' the resitors R1 and R2 is the same at all teh moments of time, thus
H1∝R1 and H2∝R2
So, H1=HR1(R1+R2) (as H=H1+H2)
Hence, H1=12CR1R1+R2ξ2

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A capacitor of capacitance C=500μF is connected to a source of constant e.m.f E=200V. Then the switch Sw was thrown over from contact 1 to contact 2. Find the amount of heat generated in a resistance R1=500Ω if R2=330Ω
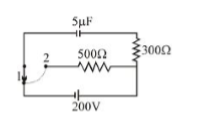
View SolutionA capacitor of capacitance 5μF is connected to a source of constant emf of 200V,Then switch was shifted to contact 2 from contact 1. Find the amount of heat generated in the 400Ω resistance.
View Solution
Knowledge Check
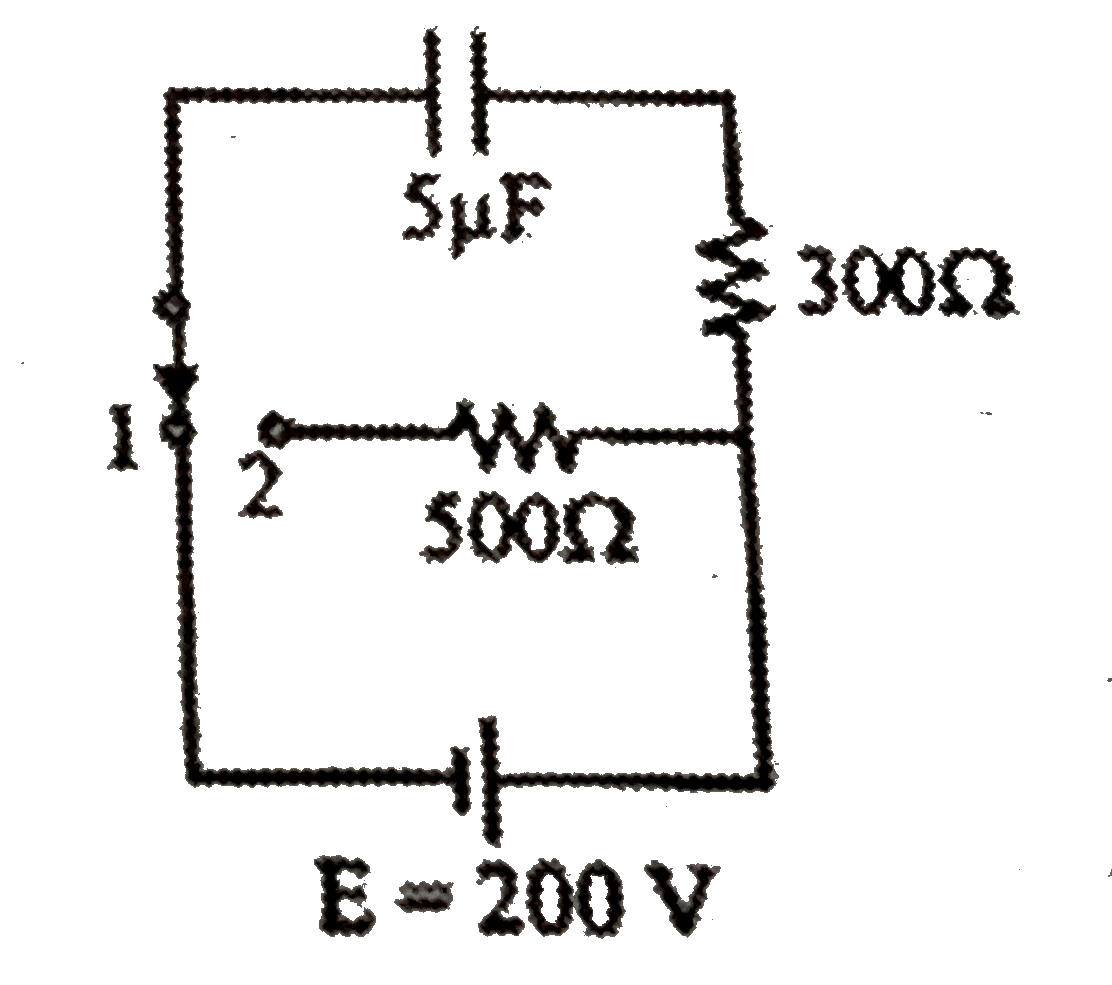
A capacitor of capacitance 5μF is connected to a source of constant emf of 200V for a long time then the swict was shifited to contact 2 form contant 1. The total amount fo heat generated in the 500ω resistance thereafter .
 A1/32JB3/32JC2/32JD5/32J
A1/32JB3/32JC2/32JD5/32JThe amount of heat generated in 500 Ω resisttance, when the kye is thrown over from contanct 1 to 2, as shown in figure, is
 A6.25×10−2JB6.25×10−3JC3.75×10−3JD3.75×10−2J
A6.25×10−2JB6.25×10−3JC3.75×10−3JD3.75×10−2J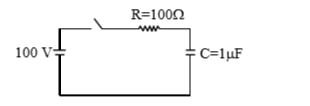
A capacitor of capacitance C=1 μF is suddenly connected to a battery of 100 volt through a resistance R=100Ω . The time taken for the capacitor to be charged to get 50 V is :
[Take ln 2 = 0.69]A1.44×10−4sB3.33×10−4sC0.69×10−4sD0.30×10−4s
To the cirucit shown in figure-3.254 a capacitor of capacitance 5μF is connected to a source of constant emf of 200V. Then the switch was shifted to contact 2 from contact 1. Find the amount of heat generated in the 400Ω resistance.
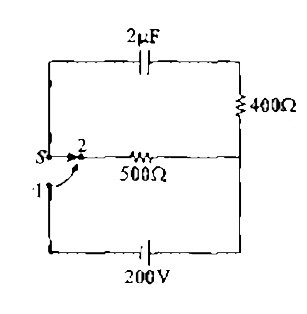
View SolutionA Capacitor of capacitance C=5μF is connected to source of emf ɛ2=200V with the switch S in the position 1 (Figure 6.2). Subsequently the switch is pushed to the position2. Find the amount of heat generated in R1=500ΩifR2=300Ω.
View SolutionA capacitor of capacitance 5μF is connected to a source of constant emf of 200V through a resistance of 300(ohm) for a long time, as shown in the figure. Then the switch was shifted to contact 1 from contact 2 . The amount of heat generated in the 500ohm resistance is H joule. Find the value of 3200H.
'(##CEN_KSR_PHY_JEE_CO20_E01_025_Q19##)'
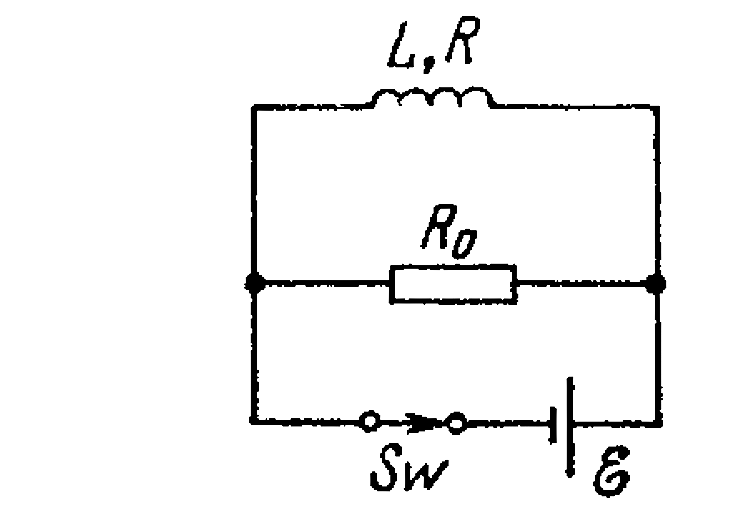
View SolutionA coil of inductance L=2.0μH and resitance R=1.0Ω is connected to a source of constant emfE=3.0V. A resistance Rs=2.0Ω is connected in parallel with the coil. Find the amount of heat generated in the coil after the swich Sw is disconnecied. The internal resistance of the source is negligible.
View SolutionA capacitor of capacitance 2μF is connected in a circuit as shown. Both cells have emf 2.5V and internal resistance 0.5Ω. Find the charge on capacitor (in μC )
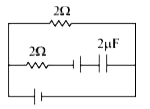
View Solution
