A wire bent as a parabola is located in a uniformed magnetic field of induaction , the vector being perpendicular to the plane . At moment a connector starts sliding translationwise from the parabola apex with a constant acceleration . Find the emf of electromagnetic induction in the loop thus formed as a function of

Obviously, from Lenz's law, the induced current and hence the induced in the loop is anticlockwise.
From Faraday's law of electromagnetic induction,
Here, ,
and from
Hence,
, using

Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Motion Of Charged Particle In Magnetic Field
Explore 36 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
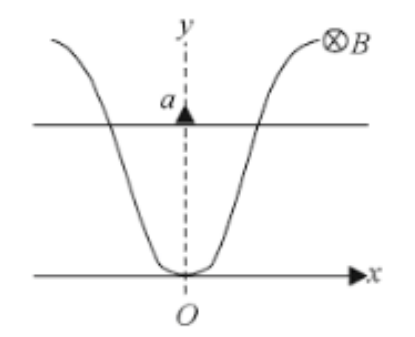
A wire bent as a parabola y=kx2 is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0, the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop -
View SolutionA conducting rod is bent as a parabola y=Kx2, where K is a constant and it is placed in a unifrom magnetic field of induction B. At t=0 a conductor of resistance per unit length λ starts sliding up on the parabola with a constant acceleration a and the parabolic frame starts rotating with constant angular frequency ω about the axis of symmetry, as shown in the figure. Find the instantaneous current induced in the rod, when the frame turns through π/4rad.
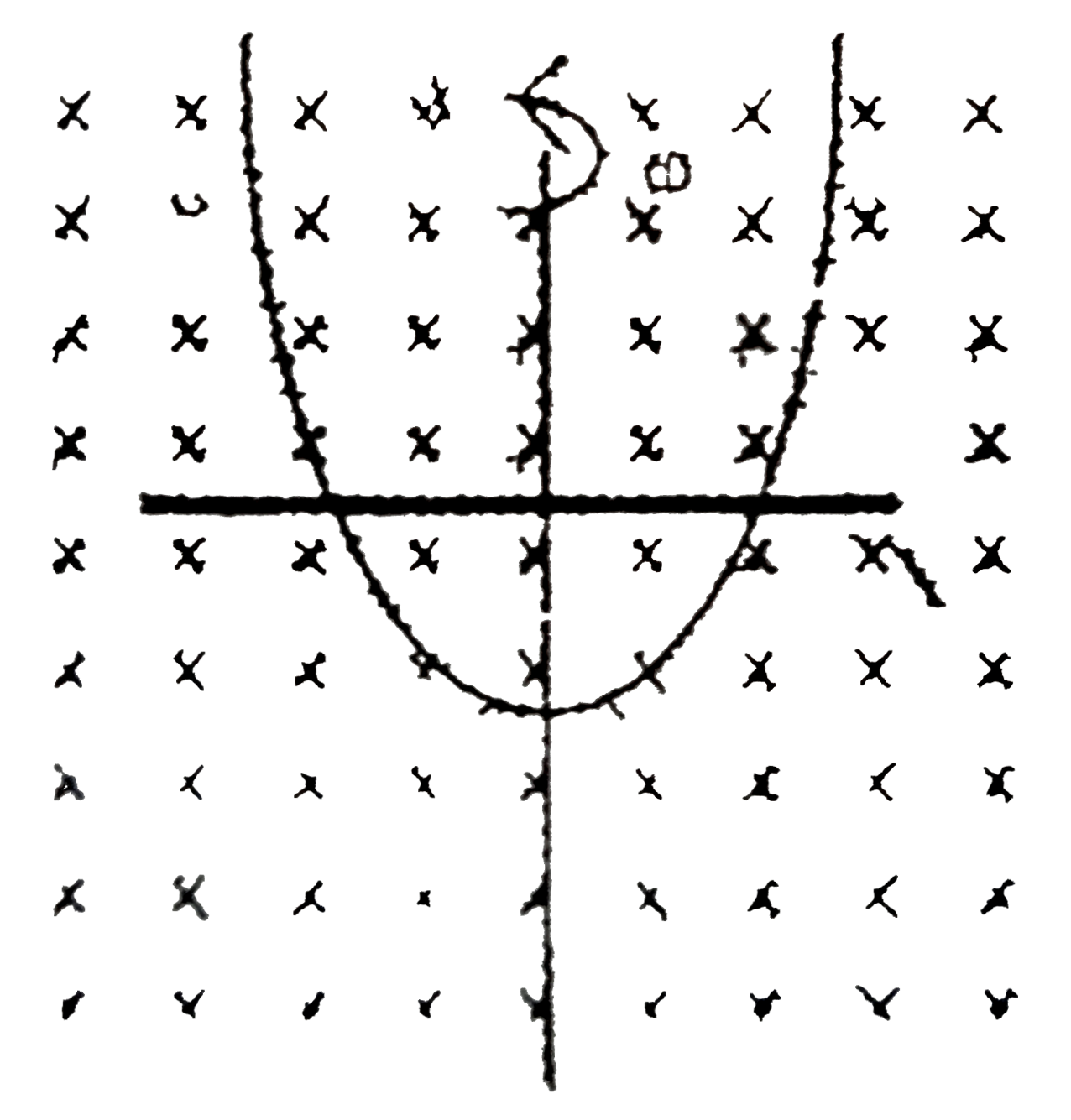
View Solution
Knowledge Check
A wire is bent in the form of a V shape and placed in a horizontal plane. There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
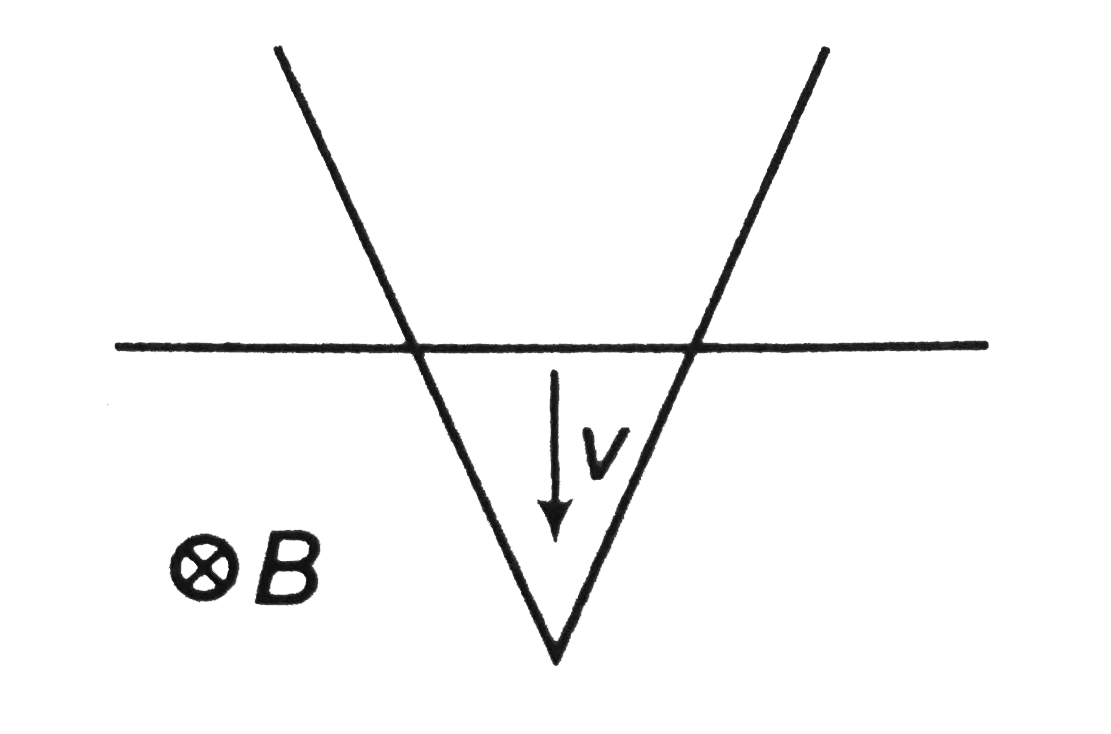 Aincrease with timeBdecrease with timeCremain constantDalways be zero
Aincrease with timeBdecrease with timeCremain constantDalways be zero
A wire loop enclosing a semi-circle of radius a=2cm is located on the boundary of a uniform magnetic field of induction B=1T (figure).At the moment t=0 the loop is set into rotation with a constant angular acceleration β=2rad/sec2 about an axis O coinciding with a line of vector B on the boundary.The emf induced in the loop as a function of time t is [x×10−4(−1)n×t]V, where n=1,2,... is the number of the half-revolution taht the loop performs at the given moment t.Find the value of x.(The arrow in the figure shows the emf direction taken to be positive, at t=0 loop was completely outside)

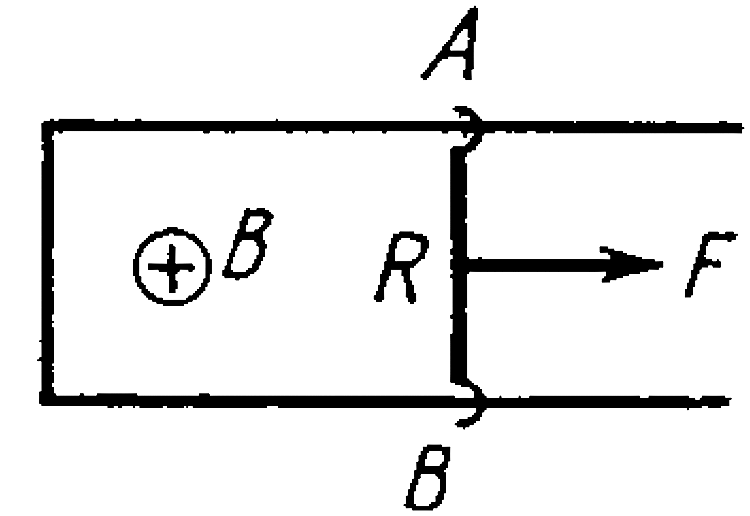
View SolutionA connector AB can slide without frictiion along a II-shaped conductor located in a horizontal plane (Fig). The connector has a length l, mass m and resistance R. The whole system is located in a unifrom magnetic field of induction B directed vertically. At the moment t=0 a constant horizontal force F starts acting on the connector shifting it translationwise to the right. Find how th e velocity o fhte connector varies with time t. The inductance of the loop and the resistance of the II-shaped conductor conductor are assumed to be negligible
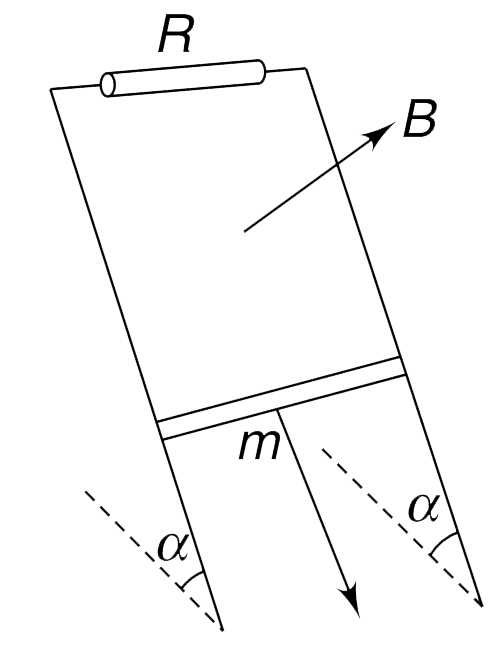
View SolutionA copper connector of massm, starting from rest, slides down two conducting bars set at angle α to the horizontal, due to gravity (see figure). At the top the bars are interconnected trhough a resistance R. The separation between the bars is equal to l. The system is located in uniform magnetic field of induction B, perpendicular to the plane in which the connectr slides. The resistance of the bars the connector and the sliding contacts, as well as the self inductance of the loop, are assumed to be negligible. The coefficient of friction between the connector and the bars is equal to 12 and α
(a) Find the steady-state velocity of the connector.
(b) How will your answer differ if the magnetic field was in opposite direction.
View SolutionA π shaped metal frame is located in a uniform magnetic field perpendicular to the plane of the conductor and varying with time at the rate (dB/dt)=0.I0T/sec . A conducting connector starts moving with an acceleration a=I0cm/sec2 along the parallel bars of the frame. The lenght o0f the connector is equal to l=20cm . Find the emf induced in the loop t=2sec after the beginnig of the motion, if at the moment t=0 the loop area and the magnetic induction are equal to zero. The inductance of the loop is to be neglected.
View SolutionA rectangular loop with a sliding conductor of length l is located in a uniform magnetic field perpendicular to the plane of loop. The magnetic induction perpendicular to the plane of loop Is equal to B. The part ad and be has electric resistance R1 and R2, respectively. The conductor starts moving with constant acceleration a0, at time t=0. Neglecting the self-inductance of the loop and resistance of conductor. Find
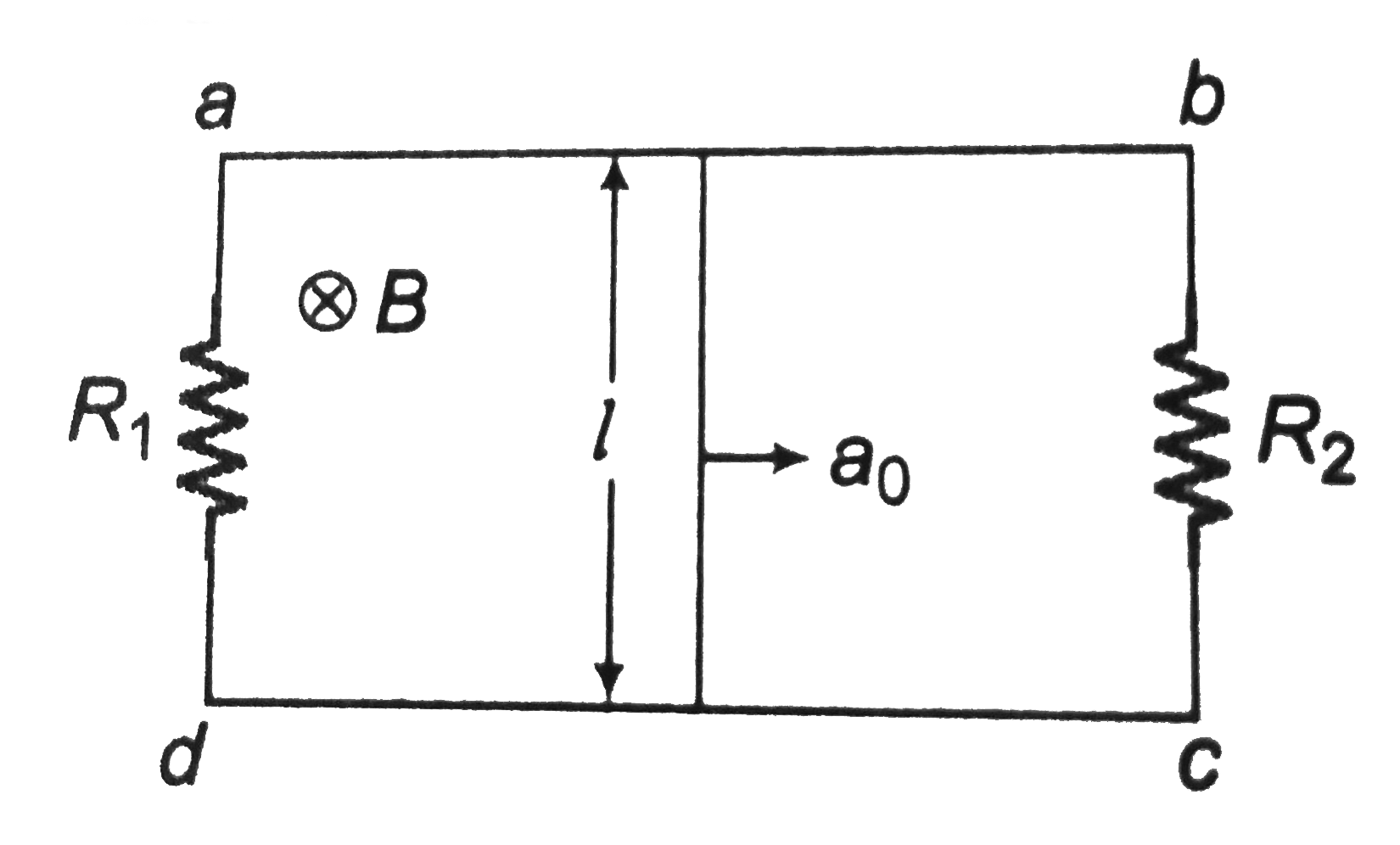
(a) the current through the conductor during its motion.
(b) the polarity of abcd terminal.
(c) external force required to move the conductor with the given acceleration.
View SolutionA copper connector of mass m slides down two smooth cooper bars, set at an angle α to the horizontal due to gravity (Fig). At the top the bars is equal to l. The system is located in a unifrom magnetic field of induction B, perpendicular to the plane in which the connector slides. The resistances of the bars, the connector and the sliding contacts, as well as the self-inductance of the loop, are assumed to be negligible. Find the steady-state velocity of the connector.

View SolutionA rectangular loop of length l and breadth b is situated in a uniform magnetic field of induction B with its plane perpendicular to the field as shown in the figure . Calculate the rate of change of magnetic flux and the induced emf if the loop is rotated with constant angular velocity ω
(a) about an axis passing through the centre and perpendicular to the loop.
(b) about an axis passing through the centre parallel to the breadth through angle 180∘ .
View Solution
