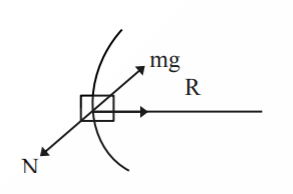
A car moves with speed v on a horizontal circular track of radius R. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground h, and the separation between its inner and outer wheel, is d. The road is dry, and the car does not skid. Show that the maximum speed the car can have without overturning is given by vmax=√gRd2h. To reduce the risk of rollover, should one increase or decrease h? Should one increase or decrease the width d of the wheel base?

When the car is on the point of rolling over, the normal force on its inside wheels is zero.
∑Fy=may:n−mg=0
∑Fx=max:f=mv2R
Take torque about the centre of mass
fh−nd2=0
Then by substitution
mv2maxRh−mgd2=0⇒vmax=√gdR2h
A wider whelbase (larger d) and a lower centre of mass (smaller h) will refuce the risk of rollover.

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.411videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.217videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
Knowledge Check
- Question 1 - Select One
A car moves with speed v on a horizontal circular track of radius R. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is h, and the separation between its inner and outer wheels is d The road is dry, and the car does not skid. The maximum speed the car can have without overturning is :
 .A√gRd2hB√gRdhC√2gRdhD√2gRd3h
.A√gRd2hB√gRdhC√2gRdhD√2gRd3h - Question 2 - Select One
A car is moving with velocity v on circular turn of radius R. Mass of the car is m. Evaluate the negative lift (FL) acting on the car
 Amv2μR−2mgBmv22μR−2mgCmv2μR−mgDmv23μR−mg
Amv2μR−2mgBmv22μR−2mgCmv2μR−mgDmv23μR−mg - Question 3 - Select One
A car is moving at a speed of 40 m/s on a circular track of radius 400 m. Its speed is increasing at the rate of 3 m/s2. The acceleration of car is
A4 m/s2B7 m/s2C5 m/s2D3 m/s2
A car of mass m travelling at speed v moves on a horizontal track. The centre of mass of the car describes a circle of radius r. If 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by
v2=grah
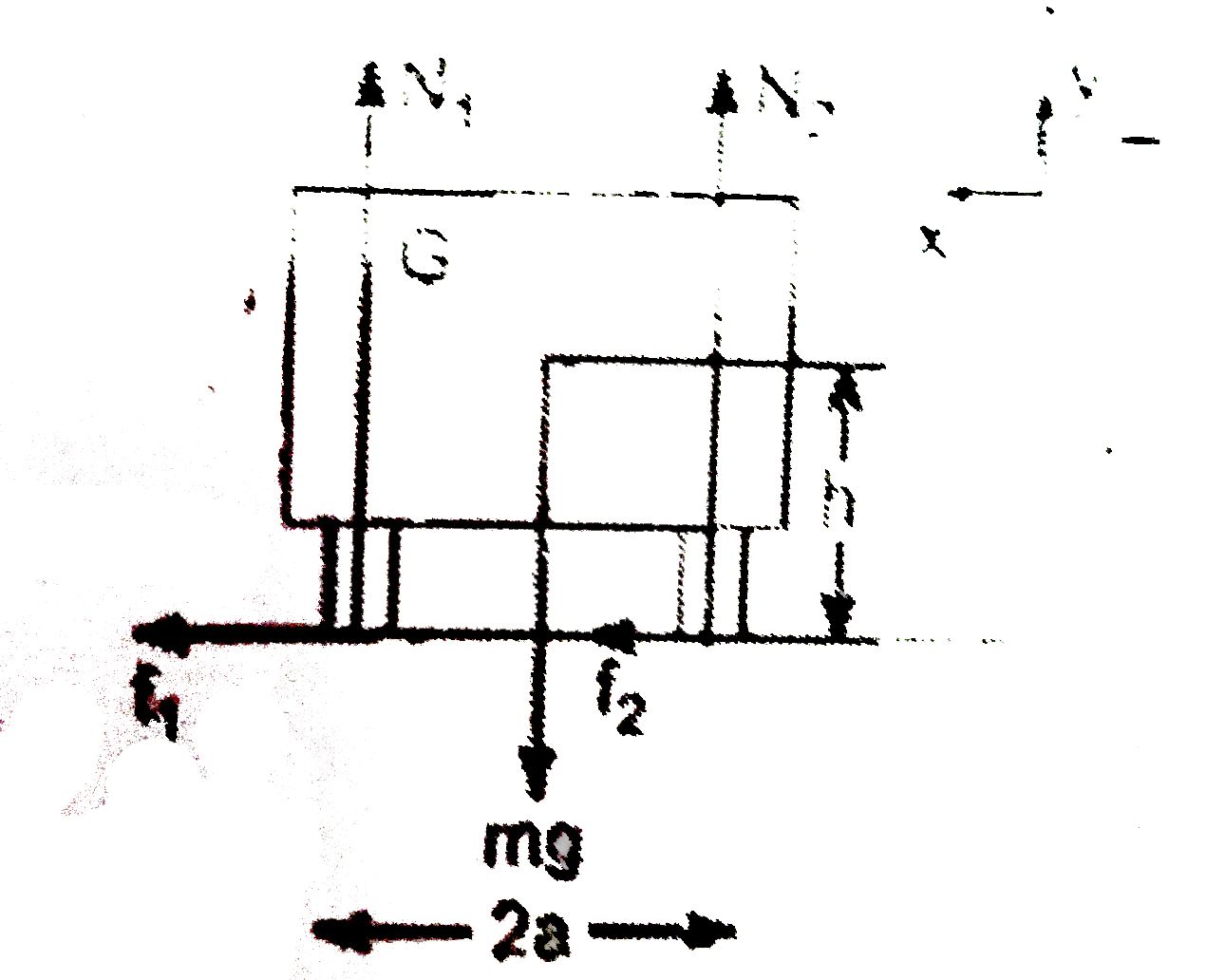 View Solution
View SolutionA car goes on a horizontal circular road of radius R. The speed of car is increasing at constant rate a m/s2. If the friction coefficient between the road and the tyre is μ, then the limiting speed of car is
View SolutionA car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tire and the road is μs=2.0, find the maximum speed the car can take without skidding.
View SolutionA car is moving with speed of 10m/s in a concave road of radius 100 m .If the mass of the car is 700 kg, then the reaction on the car tyres when it is at the lowest position will be
View SolutionA car of mass 1000 kg moves on a circular track of radius 20 . If the coefficient of friction is 0.64, then the maximum velocity with which the car can move is
View Solution

