A uniform beam of mass $m$ is inclined at an angle $θ$ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is $μ_{s}$ determine an expression for the maximum mass $M$ that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at $P$ in terms of $m, M$ and $μ_{s}$
.

Text Solution

Verified by Experts

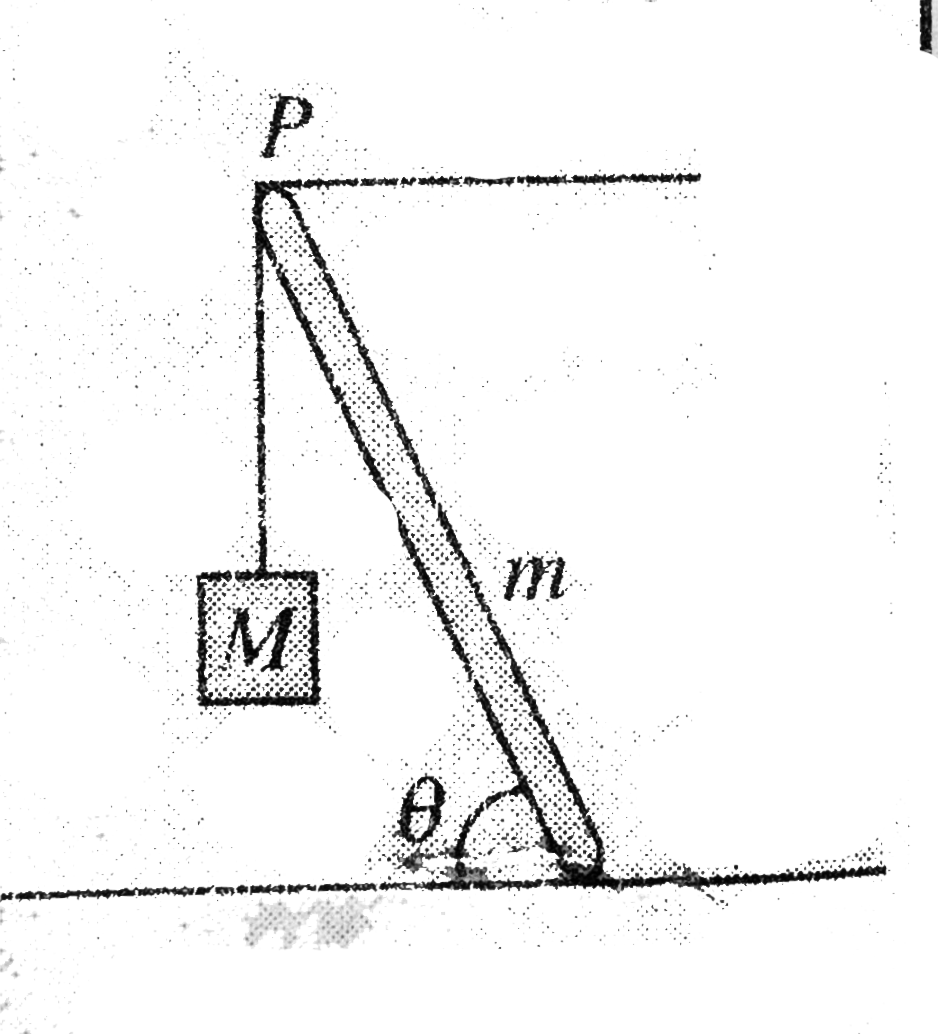We can use $\sum F_{x} = \sum F_{y} = 0$ and $\sum τ = 0$ with pivot point at the contact on the floor.

Then $\sum F_{x} = T - μ_{s} n = 0$
$\sum F_{y} = n - M g - m g = 0$
$\sum τ = M g (L cos θ) + m g (\frac{L}{2} cos θ) - T (L sin θ) = 0$
Solving the above equations gives
$M = \frac{m}{2} (\frac{2 μ_{s} sin θ - cos θ}{cos θ - μ_{s} sin θ})$
This answer is the maximum value of $M$ if $μ_{s} < cot θ$ . If $μ_{s} \geq cot θ$ , the mass $M$ can increase without limit. it has no maximum value, and part b. cannot be answered an stated either. In the case $μ_{s} < cot θ,$ we proceed.
b. At the floor we have the normal force in the $y$ -direction and frictional force in the $x$ -direction. The reaction force then is
$R = \sqrt{n^{2} + {(μ_{s} n)}_{s}^{2}} = (M + m) g \sqrt{1 + μ_{s}^{2}}$
At point $P$ , the force of the beam on the rope is
$F = \sqrt{T^{2} + {(M g)}^{2}} = g \sqrt{M^{2} + μ_{s}^{2} {(M + m)}^{2}}$

Updated on:21/07/2023

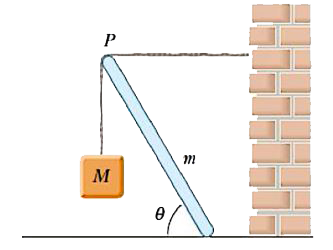
A uniform beam of mass m is
inclined at an angle $θ$ to the
horizontal. Its upper end
produces a $90^{\circ}$ bend in a very
rough rope tied to a wall, and
its lower end rests on a rough
floor(see figure). If the
coefficient of static friction
between the beam and the floor
is $μ$ then the maximum value of
M is given by the expression

A $M \leq \frac{m (2 μ - cot θ)}{2 (cot θ - μ)}$
B $M \leq \frac{μ m}{(1 - 3 μ)}$
C $M \leq \frac{m (2 μ - tan θ)}{2 (tan θ - μ)}$
D $M \leq \frac{m}{(1 - 3 μ)}$
A block of mass m is placed on a rough floor of a lift . The coefficient of friction between the block and the floor is $μ$ . When the lift falls freely, the block is pulled horizontally on the floor. What is the force of friction -
A $μ m g$
B $μ m g / 2$
C $2 μ m g$
DNone of these
A man drags an m kg crate across a floor by pulling on a rope inclined at angle $θ$ above the horizontal. If the coefficient of static friction between the floor and crate is then the tension required in the rope to start the crate moving is :
A $\frac{μ_{s} m g}{(sin θ - μ_{s} cos θ)}$
B $\frac{μ_{s} m g}{(sin θ + μ_{s} cos θ)}$
C $\frac{μ_{s} m g}{(cos θ - μ_{s} sin θ)}$
D $\frac{μ_{s} m g}{(cos θ + μ_{s} sin θ)}$