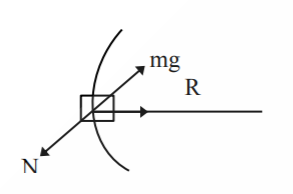
A car moves with speed $v$ on a horizontal circular track of radius $R$ . A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is $h$ , and the separation between its inner and outer wheels is $d$ The road is dry, and the car does not skid. The maximum speed the car can have without overturning is :
.

A

$\sqrt{\frac{g R d}{2 h}}$

B

$\sqrt{\frac{g R d}{h}}$

C

$\sqrt{\frac{2 g R d}{h}}$

D

$\sqrt{\frac{2 g R d}{3 h}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

(a) When the car is on the point of rolling over, the normal force on its inside wheels is zero.
$\sum F_{y} = m a_{y} : N - m g = 0$
$\sum F_{x} = m a_{x} : f = \frac{m v^{2}}{R}$
Take torque about the centre of mass :
$f h - N \frac{d}{2} = 0$
Then by substitution,
$\frac{m v^{2}_(max)}{R} h - \frac{m g d}{2} = 0 \Rightarrow v_{max} = \sqrt{\frac{g d R}{2 h}}$
A wider wheelbase (larger $d$ ) and a lower centre of mass (smaller $h$ ) will reduce the risk of rollover.
.

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If a car is to travel with a speed $v$ along the frictionless, banked circular track of radius $r$ , the required angle of banking so that the car does skid is
A $θ = {tan}^{- 1} (\frac{v^{2}}{r g})$
B $θ = {tan}^{- 1} (\frac{v}{r g})$
C $θ = {tan}^{- 1} (\frac{r^{2}}{r g})$
D $θ = {tan}^{- 1} (\frac{v^{2}}{2 r g})$
Question 2 - Select One
A car is moving with velocity v on circular turn of radius R. Mass of the car is m. Evaluate the negative lift $(F_{L})$ acting on the car
A $\frac{m v^{2}}{μ R} - 2 m g$
B $\frac{m v^{2}}{2 μ R} - 2 m g$
C $\frac{m v^{2}}{μ R} - m g$
D $\frac{m v^{2}}{3 μ R} - m g$
Question 3 - Select One
A car is moving at a speed of 40 m/s on a circular track of radius 400 m. Its speed is increasing at the rate of 3 m/ $s^{2}$ . The acceleration of car is
A4 m/ $s^{2}$
B7 m/ $s^{2}$
C5 m/ $s^{2}$
D3 m/ $s^{2}$

A2Z-ROTATIONAL DYNAMICS-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile