A car of mass m travelling at speed v moves on a horizontal track. The centre of mass of the car describes a circle of radius r. If 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by
v2=grah
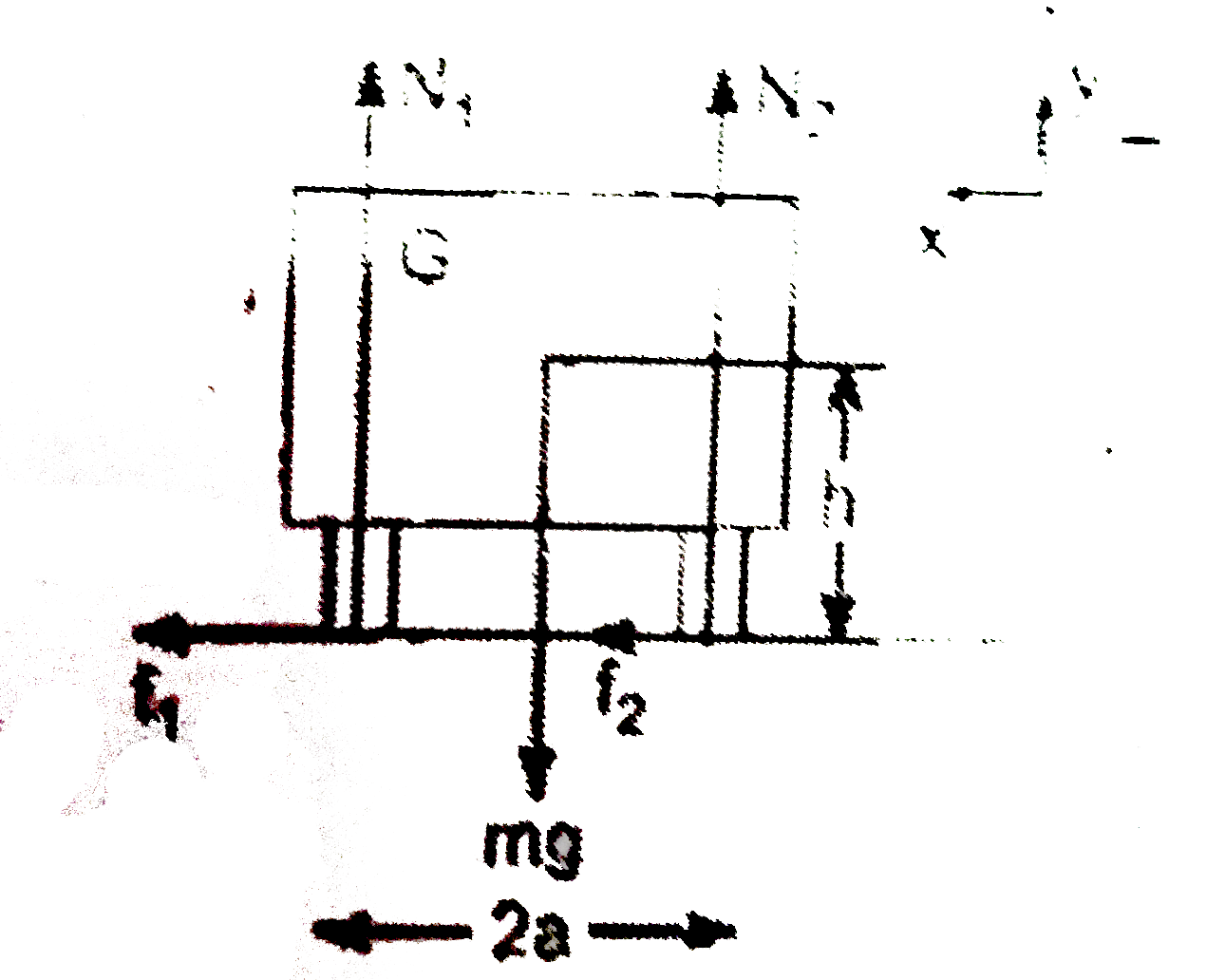
Step by step video & image solution for A car of mass m travelling at speed v moves on a horizontal track. The centre of mass of the car describes a circle of radius r. If 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by v^(2)=(gra)/h by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE83videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE41videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem4videos
UNIT AND DIMENSIONS
Similar Questions
A car of mass m travelling at speed v moves on a horizontal track so that the centre of mass describes a circle of radius r . Show that the limiting speed beyond which the car will overturn is given by
v2=grah
where 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground .View SolutionA car moves with speed v on a horizontal circular track of radius R. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground h, and the separation between its inner and outer wheel, is d. The road is dry, and the car does not skid. Show that the maximum speed the car can have without overturning is given by vmax=√gRd2h. To reduce the risk of rollover, should one increase or decrease h? Should one increase or decrease the width d of the wheel base?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A car while travelling at a speed of 72 km/hr. Passes through a curved portion of road in the form of an arc of a radius 10 m. If the mass of the car is 500 kg the reaction on the car at the lowest point P is-
A25 KNB50 KNC75 KNDNone of these - Question 2 - Select One
A car moves with speed v on a horizontal circular track of radius R. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is h, and the separation between its inner and outer wheels is d The road is dry, and the car does not skid. The maximum speed the car can have without overturning is :
 .A√gRd2hB√gRdhC√2gRdhD√2gRd3h
.A√gRd2hB√gRdhC√2gRdhD√2gRd3h - Question 3 - Select One
A car of mass m moves in a horizontal circular path of radius r metre. At an instant its speed is Vm/s and is increasing at a rate of am/sec2.then the acceleration of the car is
AV2rBaC√a2+(V2r)2D√a+(V2r)
A car of maas M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
View SolutionA car goes on a horizontal circular road of radius R. The speed of car is increasing at constant rate a m/s2. If the friction coefficient between the road and the tyre is μ, then the limiting speed of car is
View SolutionA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
View SolutionA solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
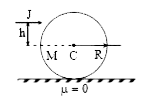 View Solution
View SolutionA car of mass m moves in a horizontal circular path of radius r meter. At an instant its speed is Vm/s and is increasing at a rate of a m/sec2. Then the acceleration of the car is:
View Solution

