A car traveling at 63 km/h hits a bridge abutment. A passenger in the car moves forward a distance of 65 cm (with respect to the road) while being brought to rest by an inflated air bag. What magnitude of force (assumed constant) acts on the passenger's upper torso, which has a mass of 41 kg ?
To solve the problem, we need to determine the magnitude of the force acting on the passenger's upper torso after the car hits the bridge abutment and the passenger is brought to rest by the airbag. We will use the principles of kinematics and Newton's second law of motion.
1. Convert the speed of the car from km/h to m/s:
Speed=63 km/h=63×1000 m3600 s=17.5 m/s
Hint: Remember that to convert km/h to m/s, multiply by 10003600.
2. Identify the initial and final velocities:
- Initial velocity (u) = 17.5 m/s (speed of the car before impact)
- Final velocity (v) = 0 m/s (the passenger comes to rest)
3. Determine the displacement during the deceleration:
Displacement(s)=65 cm=0.65 m
Hint: Always convert units to the SI system for consistency.
4. Use the third equation of motion to find acceleration:
The third equation of motion is given by:
v2=u2+2as
Rearranging for acceleration (a):
a=v2−u22s
Plugging in the values:
a=02−(17.5)22×0.65=−306.251.3≈−235.57 m/s2
Hint: The negative sign indicates that the acceleration is a deceleration (retardation).
5. Calculate the net force acting on the passenger:
Using Newton's second law:
F=m⋅a
where m is the mass of the passenger (41 kg):
F=41 kg×(−235.57 m/s2)≈−9678.37 N
Hint: The force calculated is negative due to the direction of acceleration being opposite to the motion.
6. Determine the magnitude of the force:
The magnitude of the force is:
|F|≈9678.37 N≈9.68 kN
Hint: When reporting force, it is common to express it in kilonewtons (kN) for convenience.
Final Answer:
The magnitude of the force acting on the passenger's upper torso is approximately 9.68 kN.
Speed=63 km/h=63×1000 m3600 s=17.5 m/s
- Initial velocity (u) = 17.5 m/s (speed of the car before impact)
- Final velocity (v) = 0 m/s (the passenger comes to rest)
Displacement(s)=65 cm=0.65 m
The third equation of motion is given by:
v2=u2+2as
Rearranging for acceleration (a):
a=v2−u22s
Plugging in the values:
a=02−(17.5)22×0.65=−306.251.3≈−235.57 m/s2
Using Newton's second law:
F=m⋅a
where m is the mass of the passenger (41 kg):
F=41 kg×(−235.57 m/s2)≈−9678.37 N
The magnitude of the force is:
|F|≈9678.37 N≈9.68 kN
The magnitude of the force acting on the passenger's upper torso is approximately 9.68 kN.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)36videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)5videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT5videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )5videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
Similar Questions
An autmobile travelling at 80km/h has tyres of 75.0cm diameter. What is the angualr speed of the tyres about their axles ? If the car is brought to stop uniformly in 30 complete turns of the tyres without skidding, what is the magnitude of angular acceleration of the wheels ? How far does the car move during the braking ?
View SolutionA car that weighs 1.30×104 N is initially moving at 35 km/h when the brakes are applied and the car is brought to a stop in 15 m. Assuming the force that stops the car is constant, find (a) the magnitude of the force and (b) the time required for the car experiences the same force during the braking, by what factors are (c) the stopping distance and (d) the stopping time multiplied? (There could be a lesson here about the danger of driving at high speeds.)
View Solution
Knowledge Check
- Question 1 - Select One
Direction :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
If an object of mass 2 kg and constant b=4N−sm has terminal speed vT in a liquid then time required to reach 0.63vT from start of the motion is :A2.0 secB1.26 secC0.33 secD0.5 sec - Question 2 - Select One
Direction :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
Which object has greatest terminal speed in the liquid ?AIBIICIIIDIV
An automobile traveling at 80.0km/h has tyres of 70.0 cm diameter. (a) What is the angular speed of the tires about their axles? (b) If the car is brought to a stop uniformly in 30.0 complete turns of the tyres (without skidding), what is the magnitude of the angular accelera tion of the wheels? (c) How far does the car move during the braking?
View SolutionA car is rounding a flat curve of radius R=220 m at the curve's maximum design speed v=94.0km/h. What is the magnitude of the net force on the seat cushion from a passenger with mass m=85.0 kg?
View SolutionA train starting from rest is moving along a straight track with a constant acceleration fo 2.5m/s2. A passenger at rest in the train observes a particle of mass 2kg to be at rest on the floor with which it has a coefficient of friction μs=μk=0.5 .Six seconds after the starting of the train , a horizontal force F = 13N is applied to the particle for two seconds duration. The passenger now observes the particle to move perpendicular to the direction of the train.
(a) calculate the kinetic energy of the particle with respect to the passenger at the end of 8 seconds after starting of the train.
( b) repeat the calculate of ( a) for an observer on the ground.View SolutionThe original Ferris wheel was built in 1893 by George Washington Gale Ferris, Jr., a civil engineering. The wheel, an amazing engineering construction at the time, carried 36 wooden cars, each holding as many as 60 passengers, around a circle of radius R = 38 m. The mass of each car was about 1.1×104kg. The mass of the wheel's structure was about 6.0×105kg, which was mostly in the circular grid from which the cars were suspended. The wheel made a complete rotation at an angular speed ωF in about 2 min.
(a) Estimate the magnitude L of the angular momentum of the wheel and its passengers while the wheel rotated at ωF.
(b) If the fully loaded wheel is rotated from rest to ωF in a time period Δt1=5.0s, what is the magnitude tavg of the avergae net external torque acting on it?View SolutionBrake or turn? Figure depicts an overhead view of a car's path as the car travels toward a wall. Assume that the driver begins to brake the car when the distance to the wall is d=107 m, and take the car's mass a m=1400 kg, its initial speed as v0=35 m/s and the coefficient of static friction as μs=0.50. Assume that car's weight is distributed evenly on the four wheels, even during braking (a) What magnitude of static friction is needed (between tires and road) to stop the car just as it reaches the wall? (b) What is the maximum possible static friction fs,max/ (c) If the coefficient of kinetic frictic between the (sliding) tires and the road is μk=0.40, at what speed will the car hit the wall? To avoid the crash, a driver could elect to turn the car so that it just barely misses the wall, as shown in the figure. (d) What magnitude of frictional force would be required to keep the car in a circular path of radius d and at the given speed v0, so that the car moves is a quarter circle and then parallel to the wall? (e) Is the required force less than fs.max so that a circular path is possible?
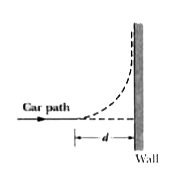 View Solution
View SolutionA worker on a railway cart is pushing a box. The cart is moving at a constant speed of 20 m/s by some external agent. The box has a mass of 25 kg, and is being pushed forward over a distance of 2m on the cart by the worker at constant acceleration, increasing its speed from 0 to 2 m/s relative to car.
(a) What will be the value of change in kinetic energy and work done by worker as calculated by Tenzing, who is standing on the cart.View Solution

