The original Ferris wheel was built in 1893 by George Washington Gale Ferris, Jr., a civil engineering. The wheel, an amazing engineering construction at the time, carried 36 wooden cars, each holding as many as 60 passengers, around a circle of radius R = 38 m. The mass of each car was about 1.1×104kg. The mass of the wheel's structure was about 6.0×105kg, which was mostly in the circular grid from which the cars were suspended. The wheel made a complete rotation at an angular speed ωF in about 2 min.
(a) Estimate the magnitude L of the angular momentum of the wheel and its passengers while the wheel rotated at ωF.
(b) If the fully loaded wheel is rotated from rest to ωF in a time period Δt1=5.0s, what is the magnitude tavg of the avergae net external torque acting on it?
(a) We can treat the wheel, cars, and passengers as a rigid object rotating about a fixed axis, at the wheel.s axle. Then Eq. (L=Iω) gives the magnitude of the angular momentum of that object. We need to find ωF and the rotational inertia I of this object.
Calculations:
Rotational inertia: To find I, let us start with the loaded cars. Because we can treat them as particles, at distance R from the axis of rotation, we know from Eq. That their rotational inertia is Ipc=MpcR2,where Mpc is their total mass. Let us assume that the 36 cars are each filled with 60 passengers, each of mass 70 kg. Then their total mass is
Mpc=36[1.1×104kg+60(70kg)]=5.47×105kg
and their rotational inertia is
Ipc=MpcR2=(5.47×105kg)(38m)2=7.90×108kg⋅m2
Next, we consider the structure of the wheel. Let us assume that the rotational inertia of the structure is due mainly to the circular grid suspending the cars.
Further, let us assume that the grid forms a hoop of radius R, with a mass Mhoop of 3.0×105kg From, the rotational inertia of the hoop is
Ihoop=MhoopR2=(3.0×105kg)(38m2)
= 4.33×108kg⋅m2
The combined rotational inertia I of the cars, passengers, and hoop is then
I=Ipc+Ihoop=7.90×108kg⋅m2+4.33×108kg⋅m2
= 1.22×109kg⋅m2
Angular speed : TO find the rotational speed ωF, we use ωavg=Δθ/Δt. Here the wheel goes through an angular displacement of Δθ=2π rad in a time period Δt=2min. Thus, we have
ωF=2πrad(2min)(60s/min)=0.0524rad/s
Angular momentum: Now we can find the magnitude L of the angular momentum with Eq.
L=IωF=(1.22×109kg⋅m2)(0.0524rad/s)
= 6.39×107kg⋅m2/s≈6.4×107kg⋅m2/s
(b) Conceptualize/Classify: The average net external torque is related to the change ΔL in the angular momentum of the loaded wheel by Eq. (→τnet=d→L/dt).
Compute: Because the wheel rotates about a fixed axis to reach angular speed ωF in time period Δt1, we can reqriye Eq.
τavg=ΔL/Δt1
The change ΔL is from zero to the answer for part (a). Thus, we have
τavg=ΔLΔt1=6.39×107kg⋅m2/s−05.0s
≈1.3×107N⋅m
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS
100 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
A disk can rotate about its central axis like a merry-go-round. Which of the following pairs of values for its initial and final angular positions, respectively, give a negative angular displacement: (a) -3 rad, +5 rad, (b) -3 rad, -7 rad, ( c) 7 rad, -3 rad?
View SolutionA tractor has rear wheels with a radius of 1.00 m and front wheels with a radius of 0.250 m. The rear wheels are rotating at 100 rev/min. Find (a) the angular speed of the front wheels in revolutions per minute and (b) the distance covered by the tractor in 10.0 min.
View SolutionA bomb is designed to explode 2.00 s after it is armed. The bomb is launched from Earth and accelerated to an unknown final speed. After reaching its final speed, however, the bomb is observed by people on Earth to explode 4.25 s after it is armed. What is the final speed of the bomb just before it explodes (in terms of c)?
View SolutionA uniform circular disc of mass 50kg and radius 0.4 m is rotating with an angular velocity of 10rads−1 about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (∈reds−1) of the system is
View SolutionA small car took off a ramp at a speed of 30 m//s . Immediately after leaving the ramp, the driver applied brakes on all the wheels. The brakes retarded the wheels uniformly to bring them to rest in 2 second. Calculate the angle by which the car will rotate about its centre of mass in the 2 second interval after leaving the ramp. Radius of each wheel is r = 0.30 m . Moment of inertia of the car along with the driver, about the relevant axis through its centre of mass is I_(M) = 80 kg m^(2) and the moment of inertia of each pair of wheels about their respective axles is 0.3 kg m^(2) . Assume that the car remained in air for more than 2 second . Also assume that before take- off the wheels rolled without sliding.
View SolutionA wheel comprises a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is

View Solution500 किग्रा द्रव्यमान की एक कार 50 मीटर त्रिज्या के वृत्त पर एकसमान चाल 36 किमी/घण्टा से गतिमान हैं । अभिकेंद्र बल हैं -
View Solution1 किग्रा द्रव्यमान तथा 50 सेमी त्रिज्या का एक वलयाकार पहिया तल पर 4 मीटर/सेकण्ड के वेग से बिना फिसले लुढ़क रहा है। पहिये का कोणीय संवेग ज्ञात कीजिये
View Solutionपिछले पहियों से चालित कार में इंजन पिछले पहियों को घूमता है तथा अगले पहिये कार के चलने के कारण घूमते है। यदि ऐसी कार क्षैतिज सड़क पर आगे की ओर धनात्मक त्वरण के साथ चल रही हो, तो
View Solutionयदि 1 किमी. की दूरी तय करने में कार के प्रत्येक पहिए को 450 चक्कर लगाने पड़ते हैं, तो प्रत्येक पहिए की त्रिज्या ज्ञात कीजिए |
View SolutionA fly wheel of mass 4 kg has moment of inertia 16kgm2, then radius of gyration about the central axis perpendicular to its plane is
View Solution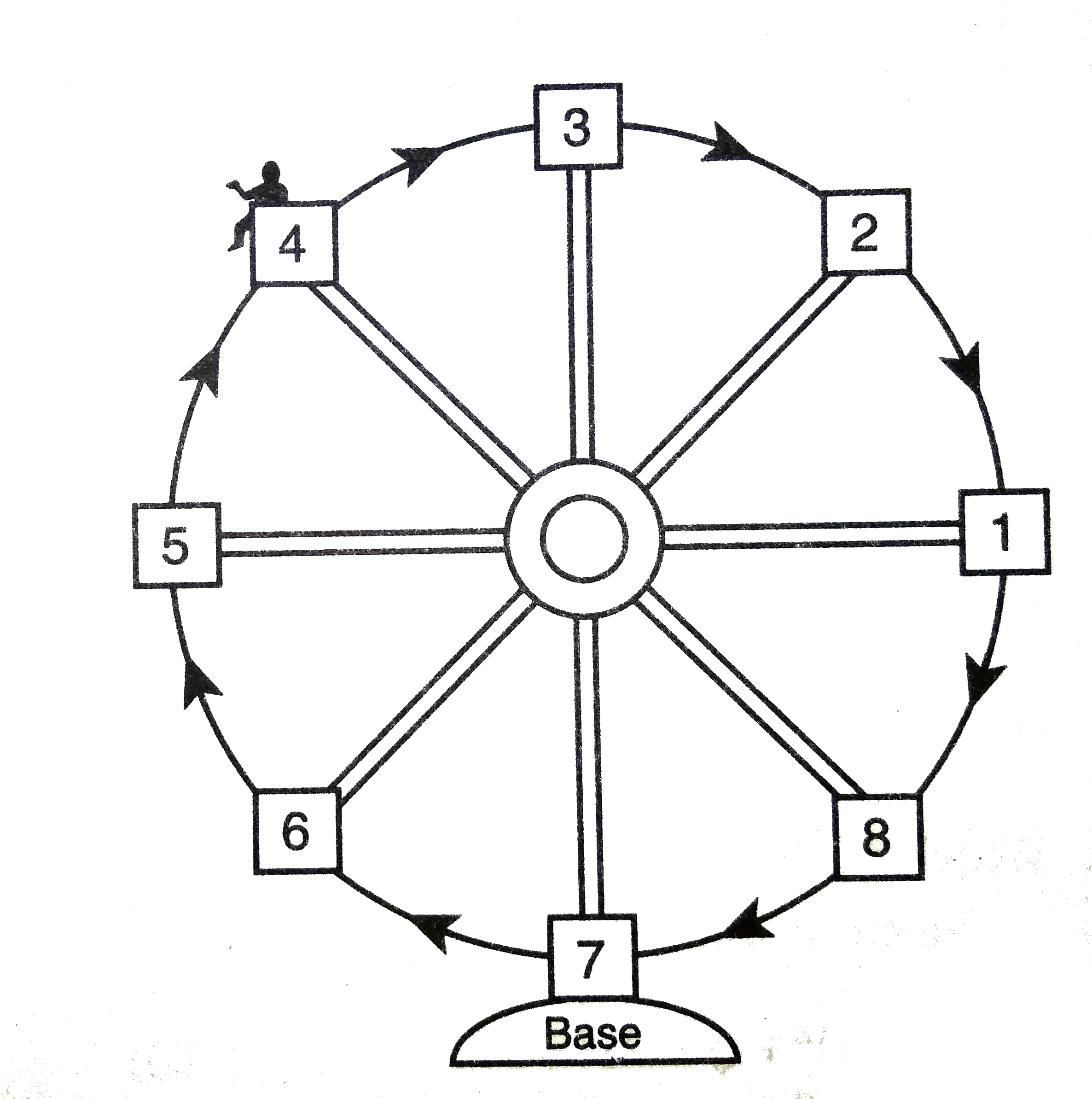
Kristine is riding in car 4 of the ferris wheel represented in the diagram above, which is 84π meters from car 8. The ferris wheel is rotating in the direction indicated by the arrows. If each of the cars are equally spaced around the circular wheel, what is the best estimate of the number of meters in the distance through which kristine's car will travel to reach the botton of the ferris wheel before her car returns to the same position?
View SolutionA wheel of mass 10 kg has a moment of inertial of 160kg−m2 about its own axis. The radius of gyration is
View SolutionA bicycle wheel of radius 0.3 m has a rim of mass 1.0 kg and 50 spokes, each of mass 0.01 kg. What is its moment of inertia about its axis of rotation ?
View SolutionA car of mass 1000 kg moves up at 40km⋅h−1 along an inclined plane of slope 150 . Coefficient of rolling friction between the road and the wheels of the car is 0.3. Find the power of the car engine.
View Solution
