A cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance of 100Ω. When a voltmeter is connected across the 100Ω resistance, the ammeter reading is 0.04A. Find the voltage reading by the voltmeter and its resistance. Had the voltmeter been an ideal one what would have been its reading?
400Ω
200Ω
300Ω
500Ω
The correct Answer is:A
To solve the problem step by step, we will analyze the circuit and apply Ohm's law and the principles of series and parallel resistances.
Step 1: Understand the Circuit Configuration
We have a cell with an EMF of 3.4 V and an internal resistance of 3 Ω. This cell is connected to:
- An ammeter with a resistance of 2 Ω
- An external resistor of 100 Ω
- A voltmeter connected across the 100 Ω resistor
Step 2: Calculate the Total Resistance in the Circuit
The total resistance Rtotal in the circuit can be calculated as follows:
1. The internal resistance of the cell (3 Ω) and the ammeter resistance (2 Ω) are in series:
Rseries=Rinternal+Rammeter=3Ω+2Ω=5Ω
2. The external resistance (100 Ω) is in parallel with the voltmeter resistance (let's denote it as Rv). However, we will first find the total current in the circuit before determining Rv.
Step 3: Calculate the Current in the Circuit
Using Ohm's law, the total voltage V is given by:
V=I⋅Rtotal
where I is the current flowing through the circuit. We know the current I=0.04A.
The total resistance in the circuit (without considering the voltmeter yet) is:
Rtotal=Rseries+Rexternal=5Ω+100Ω=105Ω
Now, using the EMF of the cell:
3.4V=0.04A⋅105Ω
This confirms that the current reading is consistent with the given values.
Step 4: Calculate the Voltage Across the 100 Ω Resistor
The voltage across the 100 Ω resistor can be calculated using Ohm's law:
V100=I⋅Rexternal=0.04A⋅100Ω=4V
Step 5: Determine the Voltmeter Resistance
Since the voltmeter is connected across the 100 Ω resistor, we can denote its resistance as Rv. The voltage reading on the voltmeter will be less than 4 V due to the loading effect of the voltmeter.
Using the voltage divider rule, we can express the voltage across the 100 Ω resistor as:
V100=RexternalRexternal+Rv⋅Vtotal
We know:
- Vtotal=3.4V
- Rexternal=100Ω
Substituting the values:
V100=100100+Rv⋅3.4
Setting V100=4V:
4=100100+Rv⋅3.4
Step 6: Solve for Rv
Cross-multiplying gives:
4(100+Rv)=3.4⋅100
400+4Rv=340
4Rv=340−400
4Rv=−60⟹Rv=−15Ω
Since resistance cannot be negative, we must have made an error in our assumptions. The voltmeter cannot read more than the total voltage available.
Ideal Voltmeter Condition
If the voltmeter were ideal (infinite resistance), it would not draw any current, and thus the voltage across the 100 Ω resistor would be equal to the total voltage:
Videal=3.4V
Conclusion
- The voltage reading by the voltmeter is less than 4 V due to the loading effect.
- The resistance of the voltmeter cannot be determined as it leads to a contradiction.
- If the voltmeter were ideal, it would read 3.4 V.
We have a cell with an EMF of 3.4 V and an internal resistance of 3 Ω. This cell is connected to:
- An ammeter with a resistance of 2 Ω
- An external resistor of 100 Ω
- A voltmeter connected across the 100 Ω resistor
The total resistance Rtotal in the circuit can be calculated as follows:
1. The internal resistance of the cell (3 Ω) and the ammeter resistance (2 Ω) are in series:
Rseries=Rinternal+Rammeter=3Ω+2Ω=5Ω
2. The external resistance (100 Ω) is in parallel with the voltmeter resistance (let's denote it as Rv). However, we will first find the total current in the circuit before determining Rv.
Using Ohm's law, the total voltage V is given by:
V=I⋅Rtotal
where I is the current flowing through the circuit. We know the current I=0.04A.
Rtotal=Rseries+Rexternal=5Ω+100Ω=105Ω
3.4V=0.04A⋅105Ω
This confirms that the current reading is consistent with the given values.
The voltage across the 100 Ω resistor can be calculated using Ohm's law:
V100=I⋅Rexternal=0.04A⋅100Ω=4V
Since the voltmeter is connected across the 100 Ω resistor, we can denote its resistance as Rv. The voltage reading on the voltmeter will be less than 4 V due to the loading effect of the voltmeter.
V100=RexternalRexternal+Rv⋅Vtotal
- Vtotal=3.4V
- Rexternal=100Ω
V100=100100+Rv⋅3.4
Setting V100=4V:
4=100100+Rv⋅3.4
Cross-multiplying gives:
4(100+Rv)=3.4⋅100
400+4Rv=340
4Rv=340−400
4Rv=−60⟹Rv=−15Ω
Since resistance cannot be negative, we must have made an error in our assumptions. The voltmeter cannot read more than the total voltage available.
If the voltmeter were ideal (infinite resistance), it would not draw any current, and thus the voltage across the 100 Ω resistor would be equal to the total voltage:
Videal=3.4V
- The voltage reading by the voltmeter is less than 4 V due to the loading effect.
- The resistance of the voltmeter cannot be determined as it leads to a contradiction.
- If the voltmeter were ideal, it would read 3.4 V.
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Integer
8 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Assertion-Reasoning
7 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type
7 Videos
Similar Questions
A cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
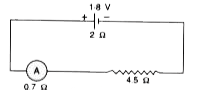
What would be the reading of the ammeter ?
View SolutionGiven that the resistance the voltmeter is 200Ω. Find the voltmeter.s reading.
View SolutionA cell of e.m.f. 2V and internal resistance 1.2.Ω is connected with an ammeter of resistance 0.8Ω and two resistors of 4.5 Ω and 9Ω as shown in the diagram below:
What would be the reading on the Ammeter?
View SolutionA cell of emf 2 V and internal resistance 1.2Ω is connected with an ammeter of resistance 0.8Ω and two resistors of 4.5Ωand9Ω as shown in the diagram below:
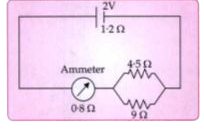
What would be the reading on the Ammeter ?
View SolutionThe emf of a cell is 6 V and internal resistance is 0.5kΩ. What will be the reading (in volt) of a voltmeter having an internal resistance of 2.5kΩ?
View SolutionThe emf of a cell is 6 V and internal resistance is 0.5kΩ The reading of a Voltmeter having an internal resistance of 2.5kΩ is
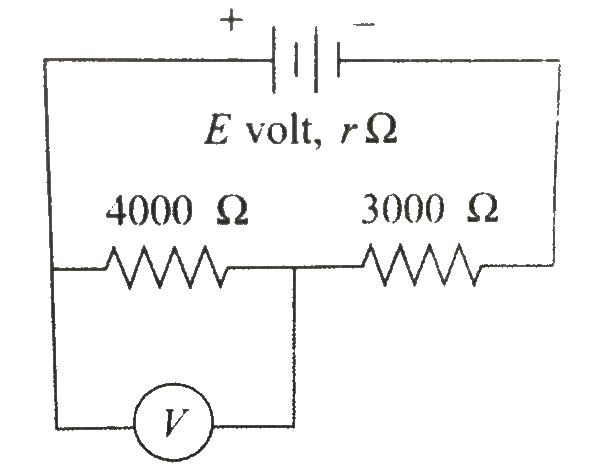
View SolutionIn Fig.6.59, when an ideal voltmetre is connected across 4000Ω resistance, it reads 30V. If the voltmeter is connected across 3000Ω resistance, it will read
View SolutionA battery of emf 1.4V and internal resistance 2Ω is connected to a resistor of 100ω resistance through an ammeter. This resistance of the ammeter is 4/3Ω. A voltmeter has also been connected to find the potential difference across the resistor.
a. Draw the circuit diagram.
b. The ammeter reads 0.02A. What is the resistance of the voltmeter?
c. The voltmeter reads 1.1V. What is the error in the reading?
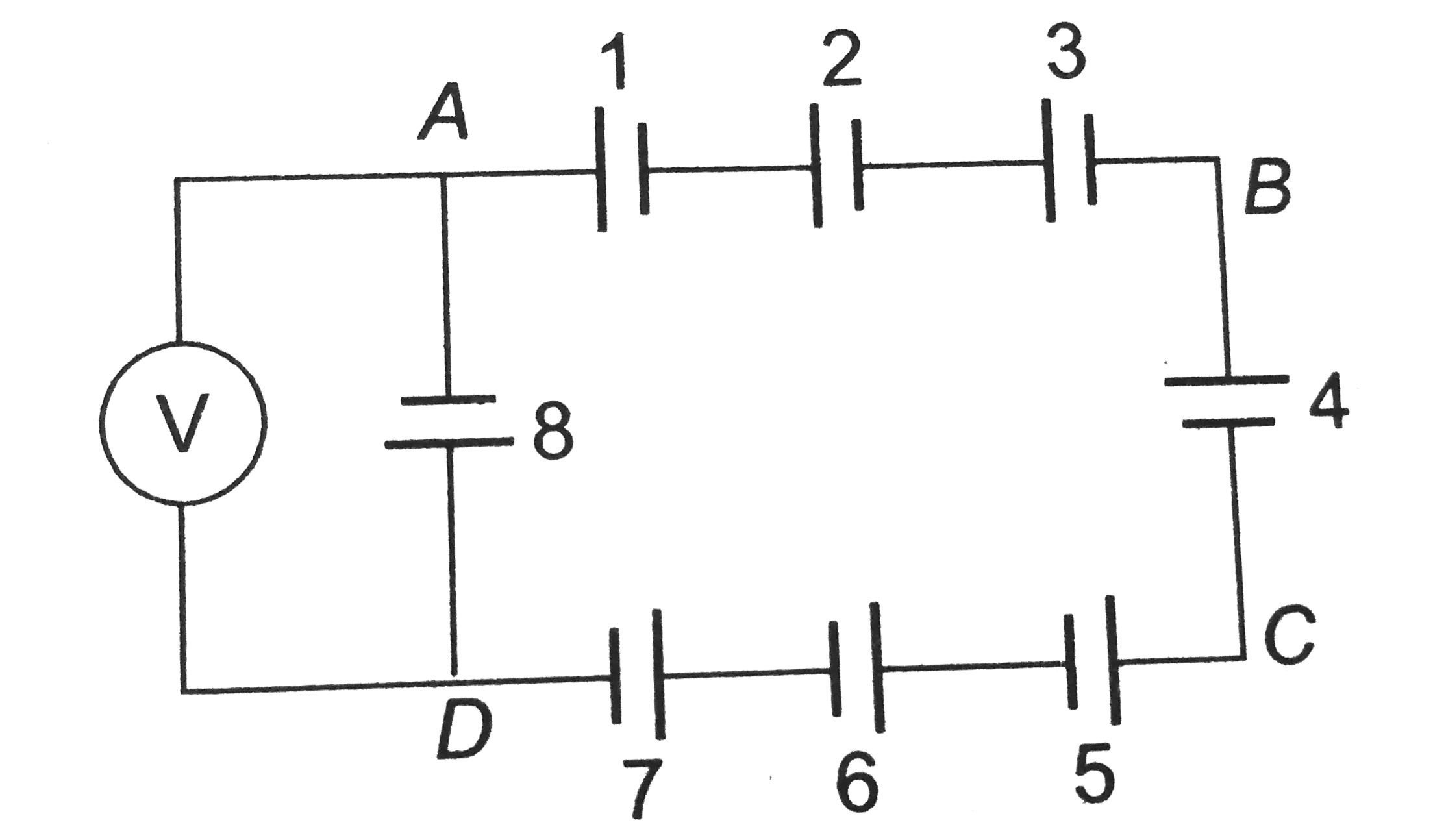
View SolutionEight cells marked 1 to 8, each of emf 5V and internal resistance 0.2Ω are connected as shown. What is the reading of ideal voltmeter ?
View SolutionTwo batteries, one of emf 18V and internal resistance 2Ω and the other of emf 12 and internal resistance 1Ω , are connected as shown. The voltmeter V will record a reading of

View Solution
