A charge of 5μC is placed at the center of a square ABCD of side 10cm. Find the work done (inμJ) in moving a charge of 1μC from A to B.
The correct Answer is:0
To solve the problem of finding the work done in moving a charge of 1μC from point A to point B in a square ABCD with a charge of 5μC placed at the center, we can follow these steps:
Step 1: Understand the Configuration
We have a square ABCD with a side length of 10cm and a charge of 5μC located at the center (point O) of the square. The points A, B, C, and D are the vertices of the square.
Step 2: Calculate the Distance from Center to Vertices
The distance from the center O to any vertex (A, B, C, or D) can be calculated using the Pythagorean theorem. The distance r from the center to a vertex is given by:
r=10cm2⋅√2=5√2cm=0.05√2m
Step 3: Calculate the Electric Potential at Points A and B
The electric potential V at a distance r from a point charge Q is given by the formula:
V=kQr
where k is Coulomb's constant (k≈9×109Nm2/C2).
For the charge at the center:
VA=VB=(9×109)⋅(5×10−6)0.05√2V
Since both points A and B are equidistant from the charge at the center, the potential at both points will be the same.
Step 4: Determine the Potential Difference
The potential difference dV between points A and B is:
dV=VB−VA=0V
Step 5: Calculate the Work Done
The work done W in moving a charge q through a potential difference dV is given by:
W=q⋅dV
Substituting the values:
W=(1×10−6)⋅0=0J
Since 1J=106μJ, the work done in microjoules is:
W=0μJ
Final Answer
The work done in moving a charge of 1μC from A to B is 0μJ.
---
We have a square ABCD with a side length of 10cm and a charge of 5μC located at the center (point O) of the square. The points A, B, C, and D are the vertices of the square.
The distance from the center O to any vertex (A, B, C, or D) can be calculated using the Pythagorean theorem. The distance r from the center to a vertex is given by:
r=10cm2⋅√2=5√2cm=0.05√2m
The electric potential V at a distance r from a point charge Q is given by the formula:
V=kQr
where k is Coulomb's constant (k≈9×109Nm2/C2).
VA=VB=(9×109)⋅(5×10−6)0.05√2V
Since both points A and B are equidistant from the charge at the center, the potential at both points will be the same.
The potential difference dV between points A and B is:
dV=VB−VA=0V
The work done W in moving a charge q through a potential difference dV is given by:
W=q⋅dV
Substituting the values:
W=(1×10−6)⋅0=0J
Since 1J=106μJ, the work done in microjoules is:
W=0μJ
The work done in moving a charge of 1μC from A to B is 0μJ.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.114videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.215videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension31videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
Similar Questions
Three points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View SolutionThree points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View Solution
Knowledge Check
- Question 1 - Select One
Four equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
AzeroB√2q2πε0aC√2qπε0aDq2πε0a
Four point charges qA=2μC,qB=−5μC,qC=2μCandqD=−5μC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1μC placed at the center of the square ?
View SolutionFour idenbtial charges +50μC each are placed, one at each corner of a square of side 2m. How much external energy is required to bring another charge of +50μC from infinity to the centre of the square
(Given 14πε0=9×109Nm2C2)View SolutionFour point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is
 View Solution
View SolutionThree charges each of +4μC are the corners B, C, D of a square ABCD of side 1m. The electric field at the centre .O. of the square is
View SolutionA point charge +10μC is at distance of 5cm directly above the center of a square of side 10 cm as shown in Fig. What is the magnitude of the electric flux through the square ? (Hint. Think of the square of the square as one face of a cube with edge 10 cm)
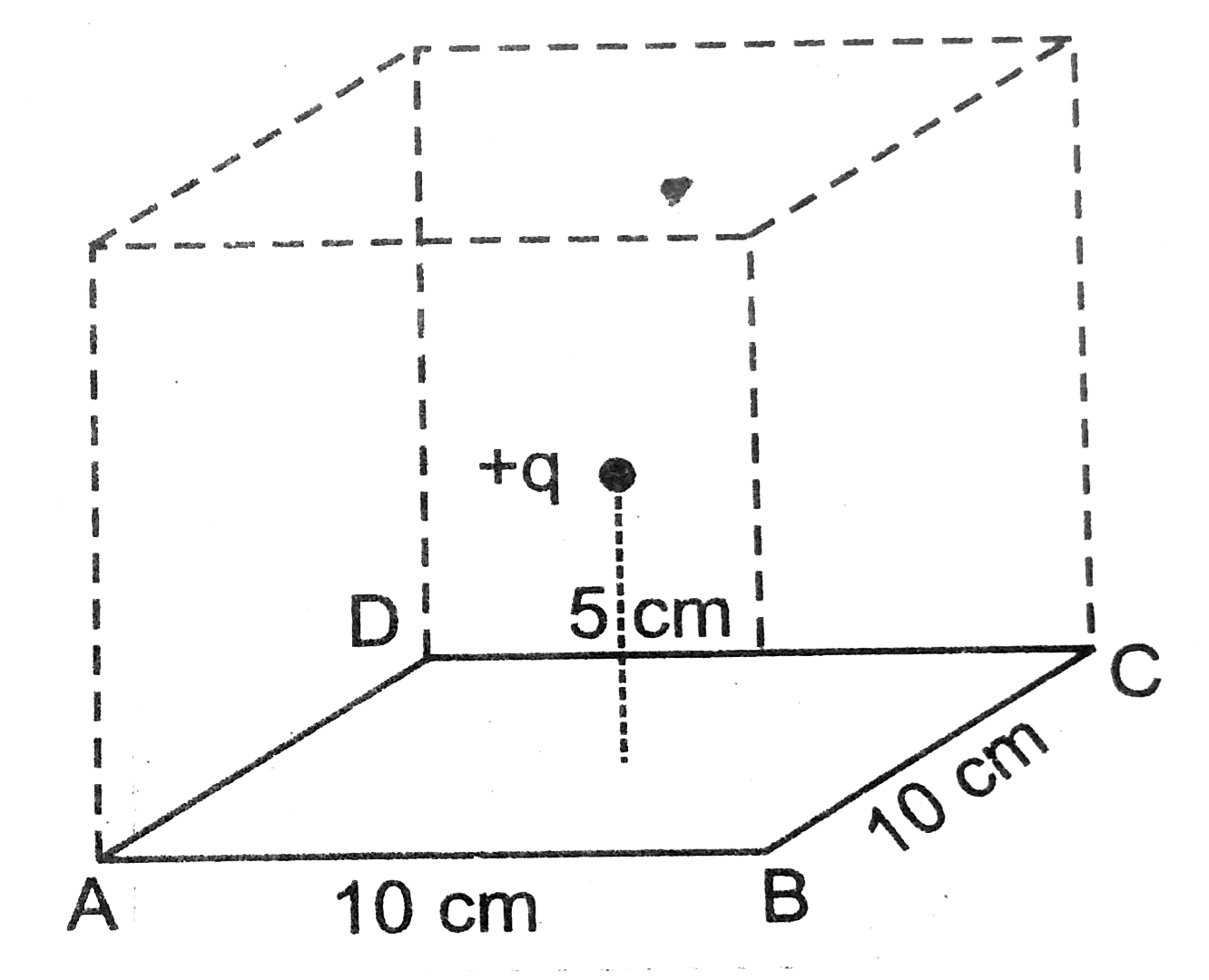 View Solution
View SolutionA charge -3 μC is placed at one corner of cube of side 9 cm . The potential at a point P which diagonally opposite as shown in fugure is
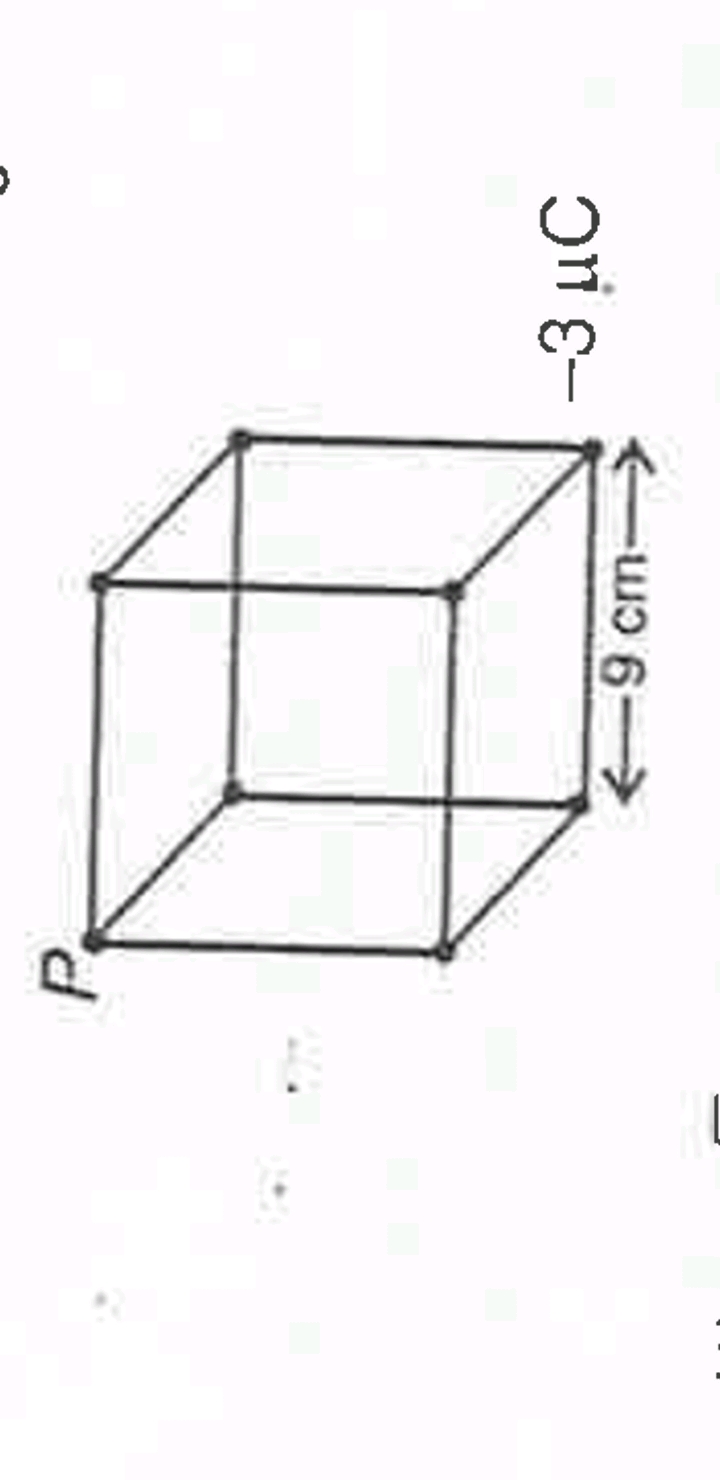 View Solution
View SolutionABC is a right - angled triangle, where ABandBC are 25cmand60cm, respectively. A metal sphere of 2cm radius charged to a potential of 9×105V is placed at B as in (Fig. 3.133). Find the amount of work done in carrying a positive charge of 1 coulomb from C to A.
 .View Solution
.View Solution

