A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of from a point P(0, 0, 3cm) to a point Q (0, 4cm, 0) via a point R(0, 6cm, 9cm).
charge located at the origin , q=8 mc =
Magnitude of a small charge, which is taken from a point p to point R to point Q,
All the points are represented in the given figure,
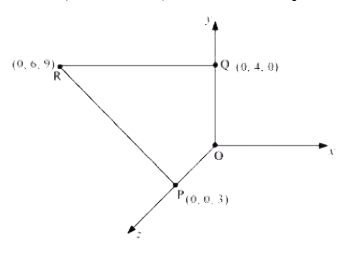
point P ios at a distance , fromt he origin along z-axis
point Q is at a distance , from the origin along y-axis .
potential at point p ,
Potential at point Q,
work done (W) by the electrostatic force is independent of the path.
Where,
=1.27 J
Therefore, work done during the process is 1.27 J.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise37videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERTCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise15videos
ELECTROMAGNETIC WAVES
- BOOK - NCERTCHAPTER - MAGNETISM AND MATTEREXERCISE - Exercise25videos
MAGNETISM AND MATTER
Similar Questions
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9C from a point P (0,0,3 cm) to a point Q (0,4 cm, 0) via a point R (0,6 cm, 9cm).
View SolutionA charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9C from a point P(0,0,3 cm) to a point Q10,4 cm, 0) via a point R(0,6 cm, 9 cm).
View Solution
Knowledge Check
- Question 1 - Select One
Calculate the work done in taking a charge −2×10−9C from A to B via C (in diagram )
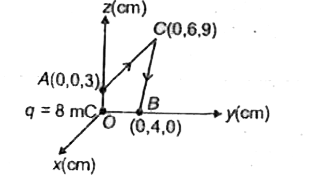 A0.2 jouleB1.2 jouleC2.2 jouleDzero
A0.2 jouleB1.2 jouleC2.2 jouleDzero - Question 2 - Select One
As per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:
 A(−qQ4πε01a2)√2aBzeroC(qQ4πε01a2)1√2D(qQ4πε01a2)1√2a
A(−qQ4πε01a2)√2aBzeroC(qQ4πε01a2)1√2D(qQ4πε01a2)1√2a - Question 3 - Select One
As per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:
 AzeroB(−qQ/4πε0)(1/a2)√2aC(qQ/4πε0)(1/a2).a/√2D(qQ/4πε0)(1/a2)√2a
AzeroB(−qQ/4πε0)(1/a2)√2aC(qQ/4πε0)(1/a2).a/√2D(qQ/4πε0)(1/a2)√2a
(a) Calculate the potential at a point P due to a charge of 4×10−7C located 9 cm away.
(b) Hence obtain the work done in bringing a charge of 2×10−9C from infinity to the point P. Does the answer depend on the path along which the charge is brought ?View SolutionTwo charges −qand+q are located at points A(0,0,−a)andB(0,0+a). How much work is done in moving a test charge from point (b,0,0) to Q(−b,0,0) ?
View SolutionCalculate the work done by electric field in moving an electron from point A(0, 2 cm) to point B(5cm, 9cm) in a region of electric field →E=104ˆjVm−1
View SolutionCalculate the potential at point (0, 7 cm) due to a point charge of 0.2 μC placed at (0, 2 cm).
View Solution(i) Can two equpotential surfaces intersect each other ? Give reason.
(ii) Two charges +qand−q are located at points A (0,0,−2)andB(0,0,2) respectively. How much work will be done in moving a test charge from point P(4,0,0) to (−5,0,0) ?View Solution

