A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
Length of the side of a cube =b
charge at each of its vertices =q
A cube of side b is shown in the following figure.
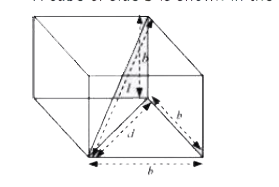
d=diagonal of one of the six faces of the cube
d2=√b2+b2=√2b2
d=b√2
l=length of the diagonal of the cube
l2=√d2+b2
=√(√2b)2+b2=√2b2+b2=√3b2
I=b√3
r=l2=b√32 is the distance betwene th centre of the cube and one of the eight vertices
The electric potential (V) at the centre of the cube is due to the presence of eight charges at the vertices
V=8q4π∈0
=8q4π∈0(b√32)
=4q√2π∈0b
Therefore, the potential at the centre of the cube is 4q√3π∈0b
The electric field at the centre of the cube, to the eight charges, gets cancelled. this is because the charges are distributed symmetrically with respect to the centre of the cube. hence, the electric field is zero at the centre.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise37videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERTCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise15videos
ELECTROMAGNETIC WAVES
- BOOK - NCERTCHAPTER - MAGNETISM AND MATTEREXERCISE - Exercise25videos
MAGNETISM AND MATTER
Similar Questions
A cube of side b has a charge g at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
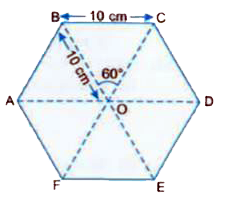
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the centre of the hexagon.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A hexagon of side 'a' has a charge 'q' at each of its vertices. The electric field at the centre of hexagon is
A0B14π∈0.qa2C14π∈0.6qa2D14π∈0.6q2a2 - Question 2 - Select One
A hexagon of side 8 cm has a charge 4μC at each of its vertices. The potential at the centre of the hexagon is
A2.7×106VB7.2×1011VC2.5×1012VD3.4×104V - Question 3 - Select One
A cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is :
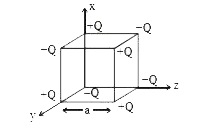 A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View SolutionA cube of side a has a charge q at each of its vertices. The potential energy of the system, of charges is "(Kq^(2))/(a)((12)/(z)+6sqrt(x)+(4)/(sqrt(y)))." Then find "x+y+z".
View SolutionGiven a cube with point charges q on each of its vertices. Calculate the force exerted on any of the charges due to rest of the 7 charges.
View SolutionThe total electric flux through a cube when a charge 8q is placed at one comer of the cube is
View SolutionThe total electric flux through a cube when a charge 8q is placed at one corner of the cube is
View Solution

