A charge Q is to be divided on two objects. What should be the values of the charges on the objects so that the force between the objects can be maximum?
To solve the problem of maximizing the force between two objects with a total charge Q, we can follow these steps:
Step 1: Define the Charges
Let one object have a charge q and the other object will then have a charge Q−q. This is because the total charge is Q.
Step 2: Write the Expression for Force
The electrostatic force F between the two charges can be expressed using Coulomb's law:
F=kq(Q−q)r2
where k is the electrostatic constant and r is the distance between the charges.
Step 3: Simplify the Expression
We can simplify the expression for force:
F=kq(Q−q)r2=k(qQ−q2)r2
Let’s denote F as a function of q:
F(q)=k(qQ−q2)r2
Step 4: Find the Maximum Force
To find the maximum force, we need to maximize the function F(q). This can be done by taking the derivative of F(q) with respect to q and setting it to zero:
dFdq=k(Q−2q)r2=0
Step 5: Solve for q
Setting the derivative equal to zero gives:
Q−2q=0
Solving for q gives:
2q=Q⟹q=Q2
Step 6: Determine the Charges on Both Objects
Since one object has charge q and the other has charge Q−q:
- Charge on the first object: q=Q2
- Charge on the second object: Q−q=Q−Q2=Q2
Conclusion
To maximize the force between the two objects, the charge Q should be divided equally between the two objects, with each receiving Q2.
---
Let one object have a charge q and the other object will then have a charge Q−q. This is because the total charge is Q.
The electrostatic force F between the two charges can be expressed using Coulomb's law:
F=kq(Q−q)r2
where k is the electrostatic constant and r is the distance between the charges.
We can simplify the expression for force:
F=kq(Q−q)r2=k(qQ−q2)r2
Let’s denote F as a function of q:
F(q)=k(qQ−q2)r2
To find the maximum force, we need to maximize the function F(q). This can be done by taking the derivative of F(q) with respect to q and setting it to zero:
dFdq=k(Q−2q)r2=0
Setting the derivative equal to zero gives:
Q−2q=0
Solving for q gives:
2q=Q⟹q=Q2
Since one object has charge q and the other has charge Q−q:
- Charge on the first object: q=Q2
- Charge on the second object: Q−q=Q−Q2=Q2
To maximize the force between the two objects, the charge Q should be divided equally between the two objects, with each receiving Q2.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
(a) Two protons are placed at some separation in vacuum. Find the ratio of electric and gravitational force acting between them.
(b) Two point charges are placed at separation 3m in vacuum. What can be the minimum force between them.
(c ) A charge Q is to be divided on two objects. What should be the value of the charges in the objects so that the force between them is maximum ?
(d) Two insulating small spheres are rubbed against each other and placed 1.6cm apart. If they attract each other with a force of 0.9N, how many electrons were transferred from one sphere to the other during rubbing ?
View SolutionA charge q is to be distributed on two conducting spheres. What should be the value of the charges on the spheres so that the repulsive force between them is maximum when they are placed at a fixed distance from each other in air ?
View Solution
Knowledge Check
If the charge on an object is doubled then electric field becomes
AhalfBdoubleCunchangedDthrice
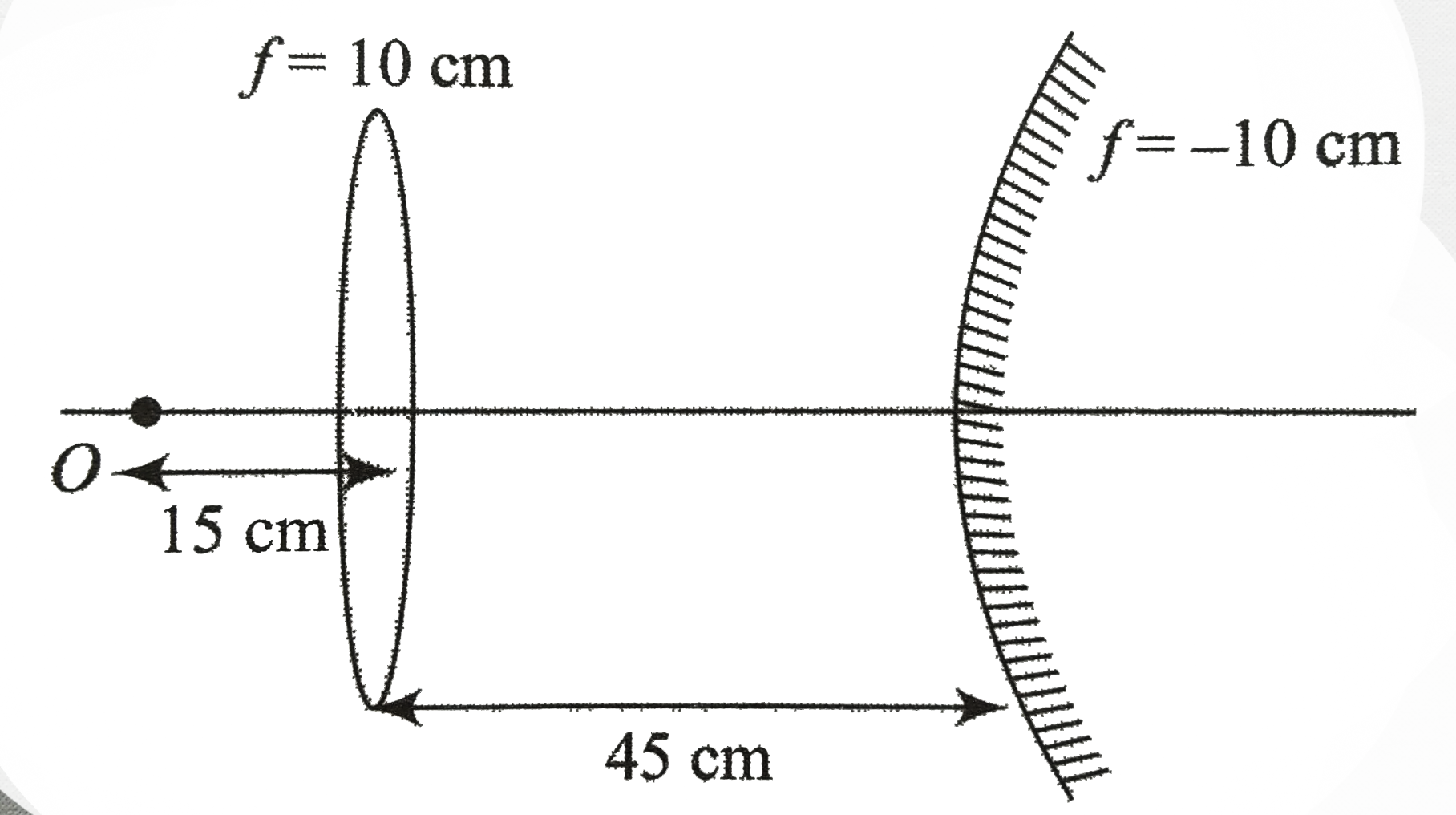
In Fig. what should be the value of d so that image is formed on the object itself .
View SolutionTwo equal charges are placed at a separtion of 1.0 m. What should be the magnitude of the charges so that the force between them equals of a 50 kg person?
View SolutionA charge Q is divided into two charge q and Q-q. The value of q such that the force between them is maximum is
View SolutionAt what distance should two charges, each equals to 1C, be placed so that the force between them equals your weight?
View SolutionAn object is placed 12cm in front of a lens to form an image on a screen. The size of the image is twice that of the object. What is the distance between the object and the image?
View SolutionA compound microscope consists of an objective of focal length 1 cm and an eyepiece of focal length 5 cm. An object is placed at a distance of 0.5 cm from the objective. What should be the separation between the lenses so that the microscope projects an inverted real image of the object on a screen 30 cm behind the eyepiece?
View SolutionAn object is placed at a distance of 30 cm from a converging lens of focal length 15 cm. A normal eye (near point 25 cm, far point infinity) is placed close to the lens on the other side. (a) Can the eye see the object clearly? (b) What should be the minimum separation between the lens and the eye so that the eye can clearly see the object? c. Can a diverging lens, placed in contact with the converging lens, help in seeing the object clearly when the eye is close to the lens?
View Solution
