A metallic loop is placed in a nonuniform magnetic field. Will an emf be induced in the loop?
To determine whether an emf is induced in a metallic loop placed in a non-uniform magnetic field, we can follow these steps:
1. Understanding the Concept of Magnetic Flux:
- Magnetic flux (Φ) through a surface is defined as the product of the magnetic field (B) and the area (A) through which it passes, considering the angle (θ) between the field and the normal to the surface:
Φ=B⋅A⋅cos(θ)
2. Identifying the Nature of the Magnetic Field:
- In this case, we have a non-uniform magnetic field. This means that the strength of the magnetic field (B) varies from one point to another within the field.
3. Determining Change in Magnetic Flux:
- For an emf (electromotive force) to be induced in the loop, there must be a change in magnetic flux through the loop over time. According to Faraday's law of electromagnetic induction:
emf=−dΦdt
- This indicates that if the magnetic flux (Φ) is constant (not changing with time), then the induced emf will be zero.
4. Analyzing the Given Situation:
- Although the magnetic field is non-uniform, if it does not change with respect to time (i.e., it is static), the magnetic flux through the loop will also remain constant.
5. Conclusion:
- Since there is no change in magnetic flux over time, we conclude that there will be no induced emf in the metallic loop placed in the non-uniform magnetic field.
Final Answer:
No, an emf will not be induced in the loop because the magnetic flux remains constant as the magnetic field is non-uniform but not changing with respect to time.
---
- Magnetic flux (Φ) through a surface is defined as the product of the magnetic field (B) and the area (A) through which it passes, considering the angle (θ) between the field and the normal to the surface:
Φ=B⋅A⋅cos(θ)
- In this case, we have a non-uniform magnetic field. This means that the strength of the magnetic field (B) varies from one point to another within the field.
- For an emf (electromotive force) to be induced in the loop, there must be a change in magnetic flux through the loop over time. According to Faraday's law of electromagnetic induction:
emf=−dΦdt
- This indicates that if the magnetic flux (Φ) is constant (not changing with time), then the induced emf will be zero.
- Although the magnetic field is non-uniform, if it does not change with respect to time (i.e., it is static), the magnetic flux through the loop will also remain constant.
- Since there is no change in magnetic flux over time, we conclude that there will be no induced emf in the metallic loop placed in the non-uniform magnetic field.
No, an emf will not be induced in the loop because the magnetic flux remains constant as the magnetic field is non-uniform but not changing with respect to time.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE
Explore 98 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:Objective 2
Explore 7 Videos
- ELECTROMAGNETIC WAVESBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Exercise
Explore 8 Videos
Similar Questions
A metallic loop is placed in a non-uniform steady magnetic field. Will an emf be induced in the loop?
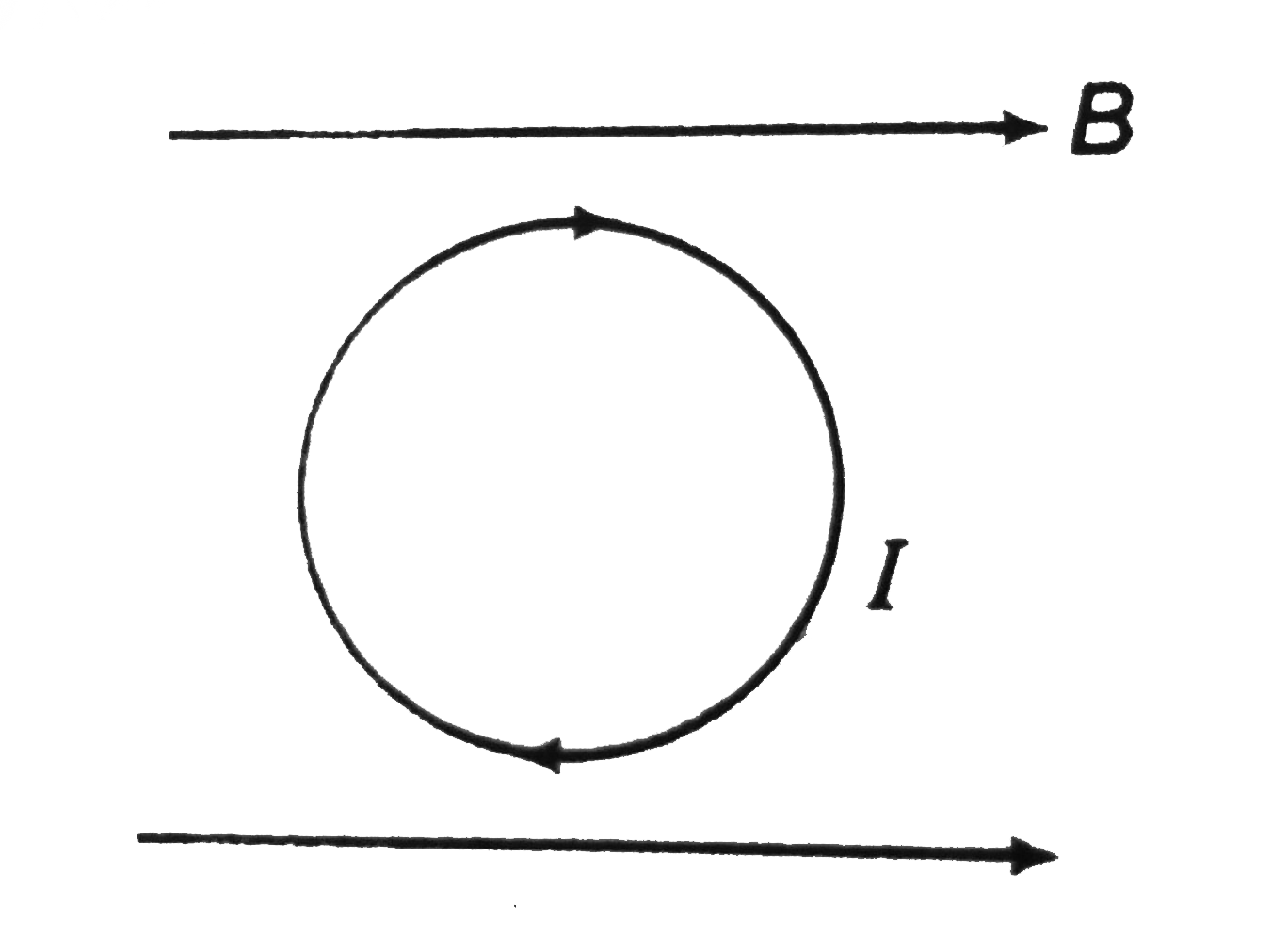
View SolutionAssertion : A current carrying loop is placed in uniform magnetic field as shown in figure. Torque in the loop in this case is zero.
Reason : Magnetic moment vector of the loop is perpendicular to paper inwards.
View SolutionA metallic loop is placed in a magnetic field. If a current is passed through it, then
View SolutionA: When a conducting loop is kept stationary in a non-uniform magnetic field an emf is induced.
R: As per Faraday's law, whenever flux changes, an emf is induced.
View SolutionA current carrying loop is placed in the non-uniform magnetic field whose variation in space is shown in fig. Direction of magnetic field is into the plane of paper. The magnetic force experienced by the loop is
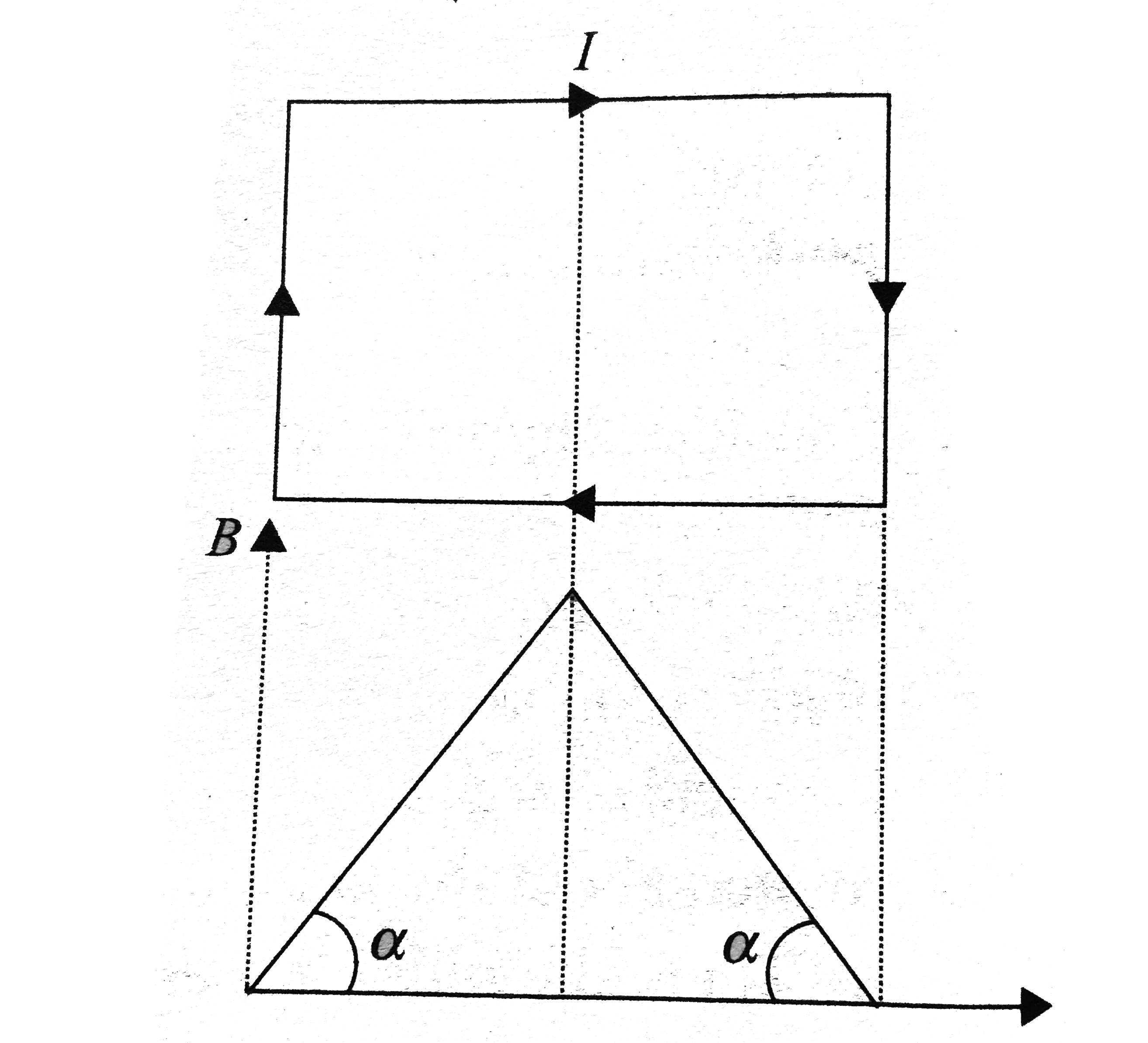
View SolutionA circular wire loop of radius r is placed in a region of uniform magnetic field B such that the plane of the loop makes an angle θ with the direction of B. In which of the following conditions, will no emf be induced in the loop?
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
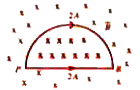
View SolutionA non planar closed loop of arbitrary shape carryign a current I is placed in uniform magnetic field. The force acting on the loop
View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m

View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m

View Solution
