A charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
∵ML=q2m
∴M=(q2m)L=(q2m)(1ω)
=(q2m)(12mR2)(ω)=qR2ω4
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:INTRODUCTORY EXERCISE
Explore 1 Video
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:SUBJECTIVE_TYPE
Explore 1 Video
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:MCQ_TYPE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEYChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
A disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionCharge Q is uniformly distributed over a nonconducting ring of radius R and mass m. It is made to rotate about an axis passing through its centre and perpendicular to its plone with an angular velocity of rotation ω. Find its magnetic dipole moment and its ratio with angular momentum.
View Solution
Knowledge Check
If a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
Amoment of inertia decreasesBmoment of inertia increasesCradius of gyration increasesDradius of gyration decreasesRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
ARBR2C√2RDR√2A charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
A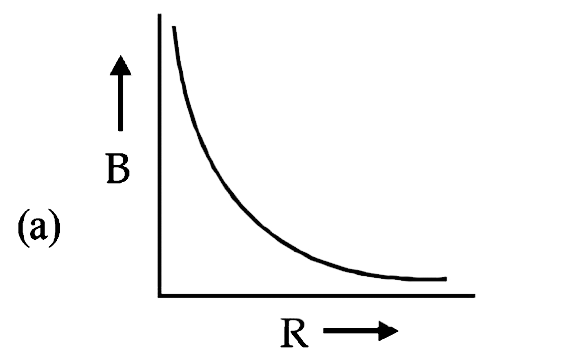 B
B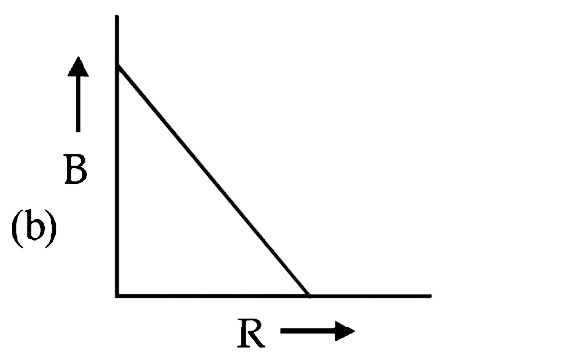 C
C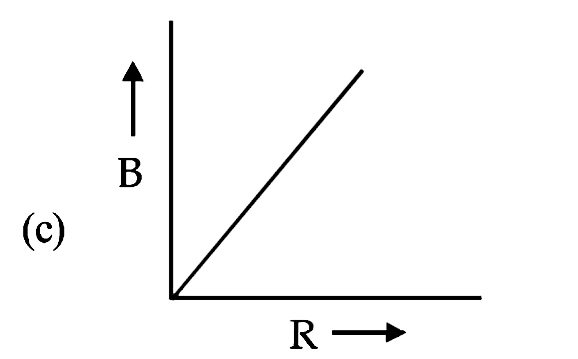 D
D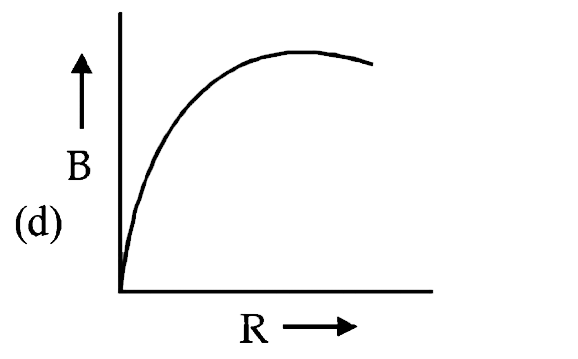
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionCharge q is uniformly distributed on a disc of radius r. If the disc is rotated with a frequency v, then magnetic field induction at the centre will be
View SolutionThe moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
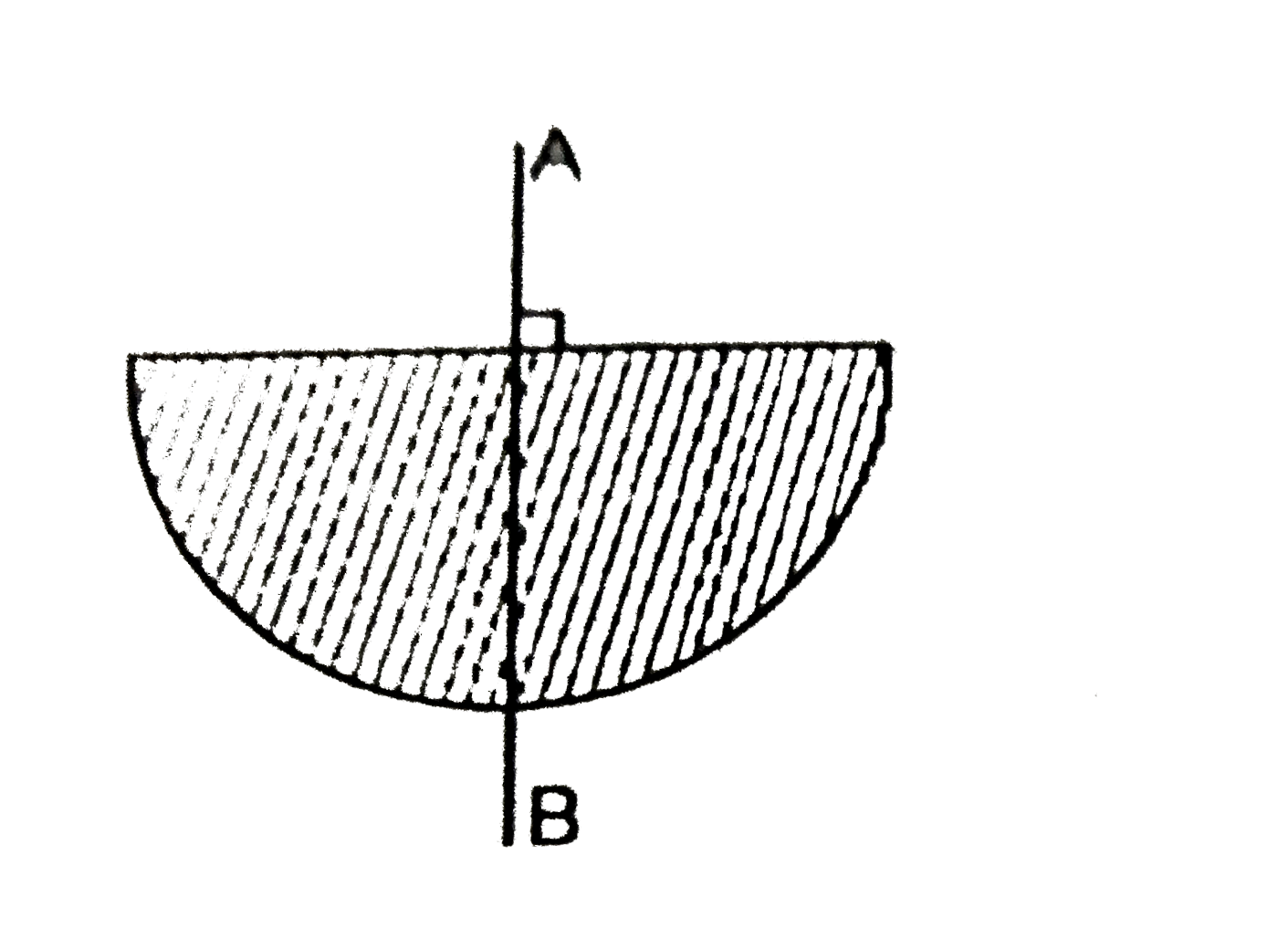
View Solution
