A charged particle of unit mass and unit charge moves with velocity $\vec{v} = (8 \hat{i} + 6 \hat{j}) m s^{- 1}$ in magnetic field of $\vec{B} = 2 \hat{k} T$ . Choose the correct alternative (s).

A

The path of the particle may be $x^{2} + y^{2} - 4 x - 21 = 0$

B

The path of the particle may be $x^{2} + y^{2} = 25$

C

The path of the particle may be $y^{2} + z^{2} = 25$

D

The time period of the particle will be 3.14 s

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, D

$r = \frac{m V}{B q} = \frac{(1) (10)}{(2) (1)} = 5 m$
$T = \frac{2 π m}{B q} = \frac{(2) (π) (1)}{(2) (1)} = π$
$= 3.14 s$
Plane of circle is perpendicular to $B$ , i.e., $x y$ -plane.

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A charged particle of specific charge $α$ moves with a velocity $\to v = v_{0} ˆ i$ in a magnetic field $\to B = \frac{B_{0}}{\sqrt{2}} (ˆ j + ˆ k)$ . Then (specific charge=charge per unit mass)
Apath of the particle is a helix
Bpath of the particle is circle
Cdistance moved by the particle in time $t = \frac{π}{B_{0} α} i s \frac{π v_{0}}{B_{0} α}$
Dvelocity of the particle after time $t = \frac{π}{B_{0} α} i s (\frac{v_{0}}{2} ˆ j + \frac{v_{0}}{2} ˆ j)$
Question 2 - Select One
A charge particle moves with velocity $\to V = A ˆ i + D ˆ j$ magnetic field . $\to B = A ˆ i + D ˆ j$ The force acting on the particle has magnitude .F Then,
AF = 0 , if aD = dA
BF = 0 , if aD = -dA
CF = 0 , if aA = -dD
D $F \propto {(a^{2} + b^{2})}^{1 / 2} \times {(A^{2} + D^{2})}^{1 / 2}$
Question 3 - Select One
A charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).

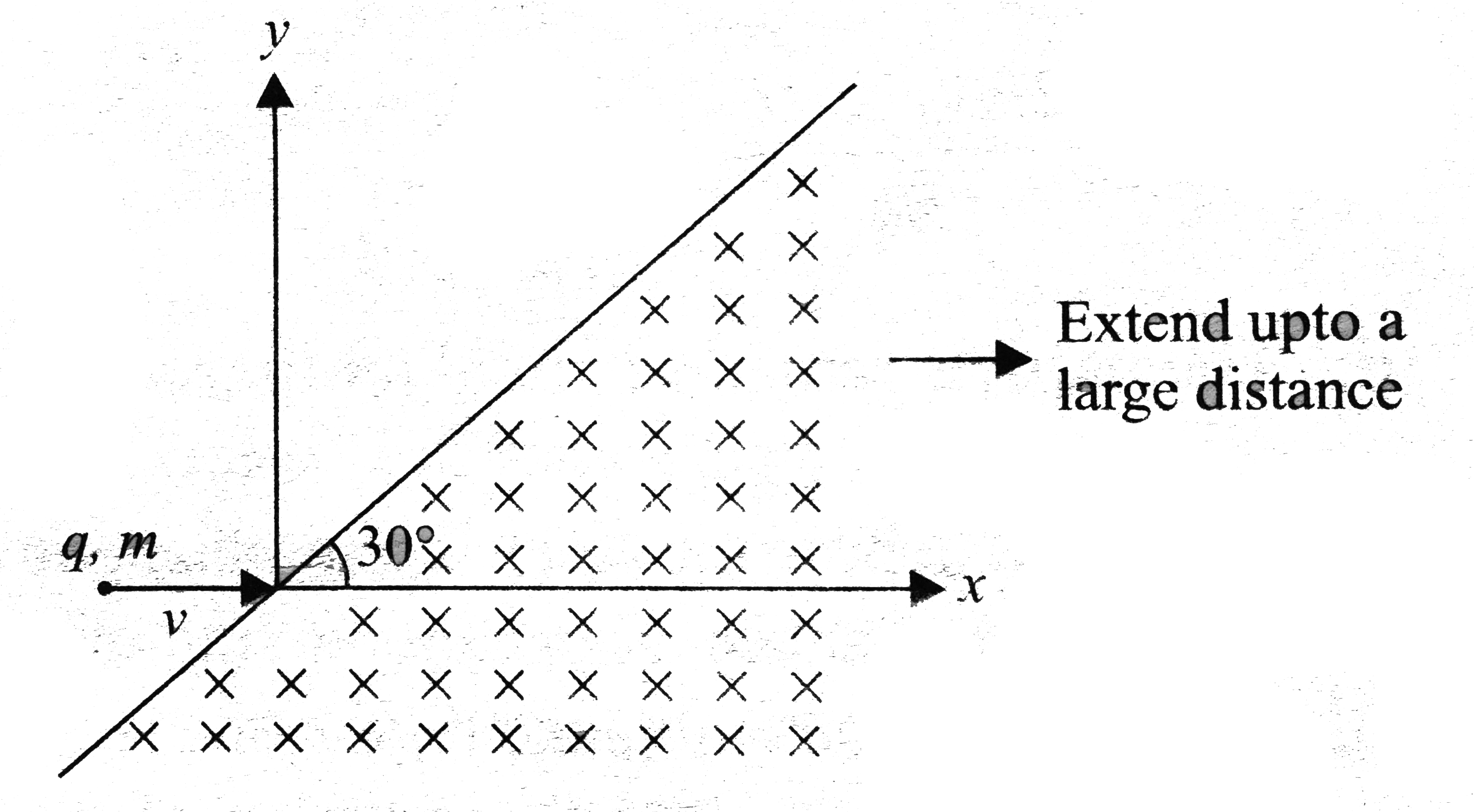AVelocity of the particle when it comes out form the magnetic field is $\to v - v {cos 60}^{\circ} ˆ i + v {sin 60}^{\circ} ˆ j$
BTime for which the particle was in magnetic field is $\frac{π m}{3 q B}$
CDistance travelled in magnetic field is $\frac{π m v}{3 q B}$
DNone of these

DC PANDEY-MAGNETICS-Exercise

Home
Ask Doubt
Profile