A circuit consisting of a capacitor with capacitance C and a resistance R connected in series was connected at the moment t=0 to a source of ac voltage V=Vmcosωt . Find the current in the circuit as a function of time t.
Here the equation is (Q is charge on the capacitor )
QC+RdQdt=Vmcosωt
A solution subject to Q=0 at t=0 is of the form ( as in the previous problem )
Q=Qm[cos(ωt−¯¯¯φ)−cos¯¯¯φe−t/RC]
Subtituting back
QmCcos(ωt−¯¯¯φ)−ωRQmsin(ωt−¯¯¯φ)
=Vmcosωt
=Vm{cos¯¯¯φ(ωt−¯¯¯φ)−sin¯¯¯φsin(ωt−¯¯¯φ)}
so Qm=CVmcos¯¯¯φ
ωRQm=Vmsin¯¯¯φ
This leads to
Qm=CVm√1+(ωRC)2,tan¯¯¯φ=ωRC
Hence I=dQdt=Vm√R2+(1ωC)2[−sinωt−¯¯¯φ+cos2¯¯¯φsin¯¯¯φe−t/RC]
The solution given in the book satisfies I=0 at t=0. Then Q=0 at t=0 but this will not satisfy the equation at t=0. Thus I=0, ( Equation will be satisfies with I=0 only if Q=0 at t=0)
With out I,I(t=0)=VmR
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A coil with active resistance R and inductance L was connected at the moment t=0 to a source of voltage V=Vmcosωt. Find the current in the coil as a function of time t.
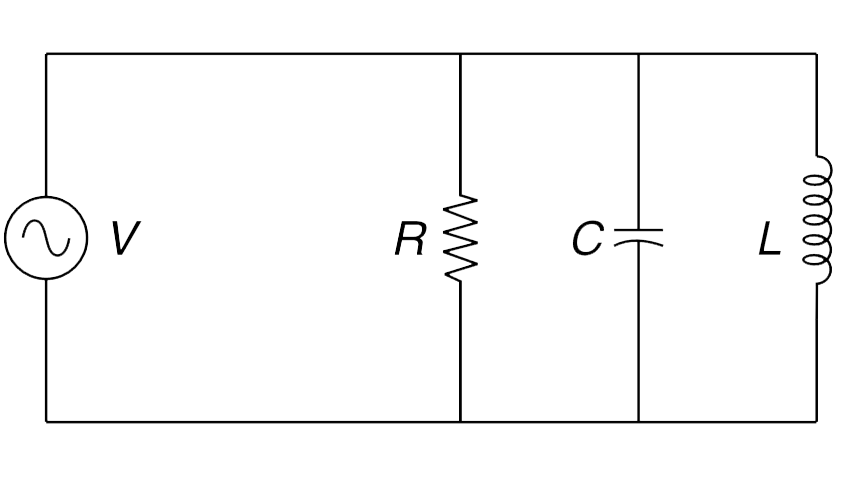
View SolutionIn the circuit shown the source voltage is given asv=V0 sin ωt. Find the current through the source as a function of time.
View Solution
Knowledge Check
An AC source is connected to the LC series circuit with V=10sin(314t). Find the current in the circuit as function of time ? (L=40mH,C=100μF)
A10sin(314t)B5.2sin(314t)C0.52sin(314t)D0.52cos(314t)
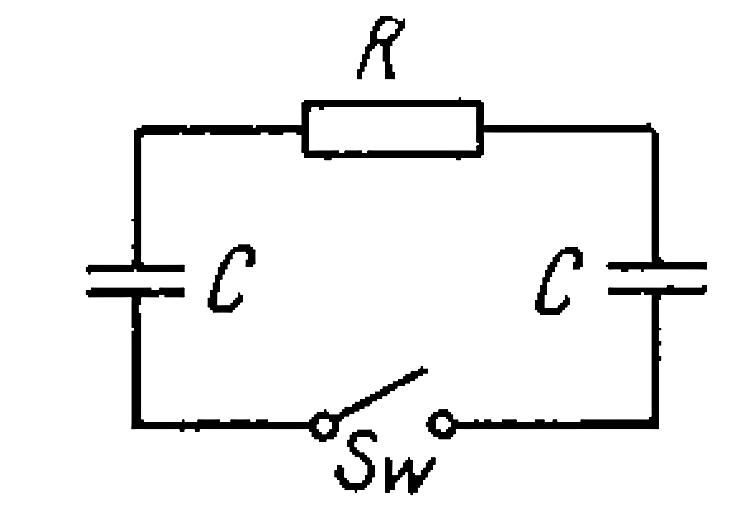
In a circuit shown in fig. the capacitance of each capacitor is equal to C and the resistance, to R One of the capacitor was connected to a voltage V0 and then at the moment t=0 was shorted by means of the swich Sw. Find:
(a) a current I in the circuit as a function of time t:
(b) the amount of generated heat provided a dependence I(t) is known.
View SolutionA circuit consists of a capacitor with capacitance C and a coil with active resistance R and inductance L connected in parallel. Find the impedane of the circuit at frequency ω of alternating voltage.
View SolutionA capacitor of unknown capacitance, a coil of inductance L, and a resistor of re-

sistance R are connected to a source of a.c. voltage E=e0cosωt (Fig. 112). The current in the circuit is I=(E0/R)cosωt.
Determine the amplitude U0 of the voltage across the capacitor plates.
View SolutionA circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage V0, and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is Imax equal to ?
View SolutionA capacitor with capacitance C and a coil with active resistance R and inductance L are connected in parallel to a source of sinusoidal voltage of frequency ω. Find the phase difference between the current fed to the circuit and the source voltage.
View SolutionAn oscillating circuit consists of a capacitor with capacitance C, a coil of inductance L with negligible resistance, and aswitch. With the switch disconnected , the capacitor was charged to a voltage Vm and then at the moment t=0 the switch was closed . Find :
(a) the current (I(t)) in the circuit as a function of time,
(b) the emf of self- inductance in the coil at the moments when the electric energy of the capacitor is equal to that of the current in the coil.
View SolutionA closed circuit consits of a source of constant and E and a choke coil of inductance L connected in series. The active resistance of the whole circuit is equal to R. At the moment t=0 the choke coil inductance was decreased abrupty η times. FInd the current in the circuit as a function of time t.
View Solution
