A circular converging lens, with diameter d = 32 mm and focal length f = 24 cm, forms images of distant point objects in the focal plane of the lens. The wavelength is λ=550nm.
(a) Considering diffraction by the lens, what angular separation must two distant point objects have to satisfy Rayleigh's criterion?
KEY IDEA
Two distant point objects P1 and P2 the lens, and a viewing screen in the focal plane of the lens. It also shows, on the right, plots of light intensity I versus position on the screen for the central maxima of the images formed by the lens. Note that the angular separation θo, of the objects equals the angular separation θi of the images. Thus, the images are to satisfy Rayleigh.s criterion, these separations must be given by Eq. 35-64 (for small angles).
Calculations: From Eq. 35-62, we obtain
θo=θi=θR=1.22λd
(1.22)(550×10−9m)32×10−3m=2.1×10−5 rad. (Answer)
Each central maximum in the two intensity curves is centered on the first minimum of the other curve.

Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT6videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PROBLEMS61videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)6videos
HYDROGEN ATOM
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)4videos
MAGNETIC FIELDS DUE TO CURRENTS
Similar Questions
A circular converging lens, with diameter d = 32 mm and focal length f = 24 cm, forms images of distant point objects in the focal plane of the lens. The wavelength is λ=550nm.
What is the separation Ar of the centers of the images in the focal plane? (That is, what is the separation of the central peaks in the two intensity-versus-position curves?)View SolutionFind the focal length of the lens used to focus an image of distant object on focal plane of the lens if the radius of central bright dot is 5μm, when it illuminated by ray of wavelength 400 nm and the radius of the circular aperture is 2.5 cm.
View Solution
Knowledge Check
- Question 1 - Select One
A lens ( focal length 50cm ) forms the image of a distant object which subtends an angle of 2 milliradian at the lens. What is the size of the image ?
A5mmB1mmC0.5mmD0.1mm - Question 2 - Select One
A lens ( focal length 50cm ) forms the image of a distant object which subtends an angle of 2 milliradian at the lens. What is the size of the image ?
A5 mmB1 mmC0.5mmD0.1mm - Question 3 - Select One
A thin biconvex lens of focal length f=25cm forms a real image of a real object an a screen. The object is separated by 5cm from the lens. The screen is drawn closer to the lens by a distance 18cm. Through what distance (approximately) must the object be shifted so that its image is again formed on the screen ?
A0.5mm toward leftB0.25mm toward leftC2.5mm toward leftD1.4mm toward left
Find the focal length of the lens used to focus an image of distant object on focal plane of the lens if the radius of central bright dot is 5μm, when it illuminated by ray of wavelength 400 nm and the radius of the circular aperture is 2.5 cm.
View SolutionA concave lens of focal length f forms an image which is n times the size of the object What is the distance of the object from the lens in terms of f and n?
View SolutionIn the figure shown ‘O’ is point object. AB is principal axis of the converging lens of focal length F. Find the distance of the final image from the lens.
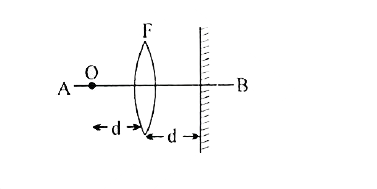 View Solution
View SolutionThe least distance between a point object and its real image formed by a convex lens of focal length F is
View SolutionAn object is placed first at infinity and then at 20 cm from the object side focal plane of a convex lens. The two images thus formed are 5 cm apart the focal length of the lens is
View Solution

